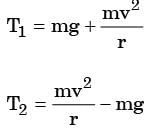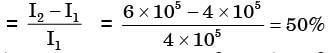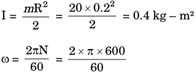All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Tests  >  Past Year Questions: Translational And Rotational Motion - Mechanical Engineering MCQ

Past Year Questions: Translational And Rotational Motion - Mechanical Engineering MCQ


Test Description

15 Questions MCQ Test - Past Year Questions: Translational And Rotational Motion

Past Year Questions: Translational And Rotational Motion for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Past Year Questions: Translational And Rotational Motion questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Past Year Questions: Translational And Rotational Motion MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Past Year Questions: Translational And Rotational Motion below.
Solutions of Past Year Questions: Translational And Rotational Motion questions in English are available as part of our course for Mechanical Engineering & Past Year Questions: Translational And Rotational Motion solutions in Hindi for Mechanical Engineering course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Past Year Questions: Translational And Rotational Motion | 15 questions in 15 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study for Mechanical Engineering Exam | Download free PDF with solutions
Past Year Questions: Translational And Rotational Motion - Question 1
Save

AB and CD are two uniform and identical bars of mass 10 kg each, as shown. The hinges at/A and B are frictionless. The assembly is released from rest and motion occurs in the vertical plane. At the instant that the hinge B passes the point B, the angle between the two bars will be

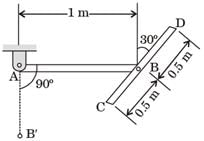
[1996]

Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 1

θ = 60° will remain same as weight mg of the rod CD passes through hinge point B so that there will be no torque in rod CD with respect to B.

Past Year Questions: Translational And Rotational Motion - Question 2
Save

A car moving with uniform acceleration covers 450 m in a 5 second interval, and covers 700 m in the next 5 second interval. The acceleration of the car is

[1998]

Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 2

For t1 =5 secs, S1 = 450 m 
and for t2 = 5 secs  S2 = 700 m
From the relation S = ut + 1/2 at2
450 = 5u + 1/2 × a × 25 [since initial velocity = u]
or 450 = 5u + 25a/2     (i)
Also after first 5 seconds, velocity of car,
v = u + at
= u + 5a.
After first 5 seconds, u + 5a will be the initial velocity for next 5 seconds, therefore
700 = (4 + 5a)5 + 1/2a × 25
= 20 + 25a + 25a/2
From equation (i), we have
700 = (5u + 25a/2) + 25a = 450 + 25a, a = 10 m/sec2.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Past Year Questions: Translational And Rotational Motion - Question 3
Save

The time variation of the position of a particle in rectilinear motion is given by x = 2t3 + t2 + 2t. If v is the velocity and a is the acceleration of the particle in consistent units, the motion started with

[2005]

Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 3

Given x= 2t3 + t2 + 2t
Velocity : v = dx/dt = 6t2 + 2t + 2
At the start of motion, t = o
V = 0 + 0 + 2
V = 2 m/s
Acceleration; a = dv/dt = 12t + 2
at t = 0
a = 0 + 2
∴ a = 2 m/s2

Past Year Questions: Translational And Rotational Motion - Question 4
Save

A simple pendulum of length of 5 m, with a bob of mass 1 kg, is in simple harmonic motion. As it passes through its mean position, the bob has a speed of 5 m/s. The net force on the bob at the mean position is

[2005]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 4

The net force at the mean position will be zero.

Past Year Questions: Translational And Rotational Motion - Question 5
Save

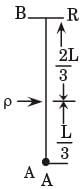
A uniform rigid rod of mass M and length L is hinged at one end as shown in the adjacent figure. A force P is applied at a distance of 2L/3 from the hinge so that the rod swings to the right. The horizontal reaction at the hinge is

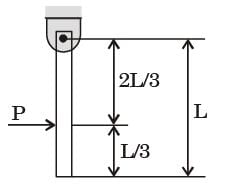
[2009]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 5


Moment about A is zero
∴ R × L = P × L/3

Past Year Questions: Translational And Rotational Motion - Question 6
Save

A and B are the end points of a diameter of a disc rolling along a straight line with a counter clockwise angular velocity as shown in figure. Referring to the velocity vectors 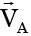 and 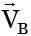 shown in the figure

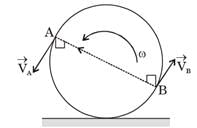
[1990]
Past Year Questions: Translational And Rotational Motion - Question 7
Save

The cylinder shown below rolls without slipping. Toward which of the following points is the acceleration of the point of contact on the cylinder directed?

[1993]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 7

Acceleration of the point of contact A acts towardsgeometric centre.

Past Year Questions: Translational And Rotational Motion - Question 8
Save

A stone of mass m at the end of a string of length l is whirled in a vertical circle at a constant speed. The tension is the string will be maximum when the stone is

[1994]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 8



T1 > T2
Maximum tension will be maximum at the bottom

Past Year Questions: Translational And Rotational Motion - Question 9
Save

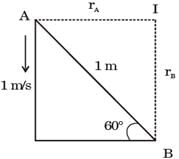
A rod of length 1 m is sliding in a corner as shown in figure. At an instant when the rod makes an angle of 60 degrees with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at the instant is

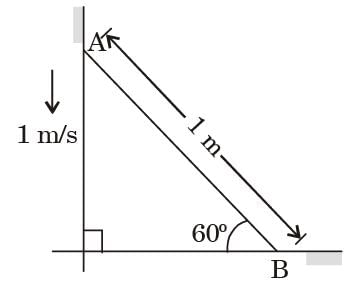
[1996]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 9


VA = rA ω
1 = 1 cos 60° × ω
ω = 2rad/sec

Past Year Questions: Translational And Rotational Motion - Question 10
Save

As shown in figure, a person A is standing at the centre of a rotating platform facing person B who is riding a bicycle, heading East. They relevant speeds and distances are shown in given figure person, a bicycle, heading East. At the instant under consideration, what is the apparent velocity of B as seen by A?

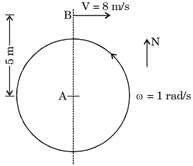
[1999]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 10

Relative velocity = 8

Past Year Questions: Translational And Rotational Motion - Question 11
Save

A rigid body shown in the fig. (a) has a mass of 10 kg. It rotates with a uniform angular velocity w. A balancing mass of 20 kg is attached as shown in fig. (b). The percentage increase in mass moment of inertia as a result of this addition is

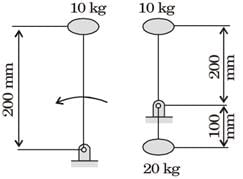
[2004]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 11


I1 = 10 × (200)2 = 4 × 105
I2 = 10 × (200)2 + 20 × (100)2 = 6 × 105
∴ % increase in moment of inertia

Past Year Questions: Translational And Rotational Motion - Question 12
Save

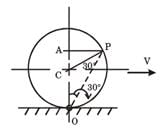
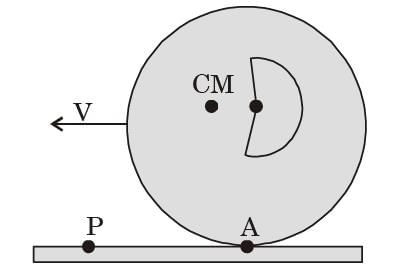
A circular disk of a radius R rolls without slipping at a velocity V. The magnitude of the velocity at point P (see figure) is:

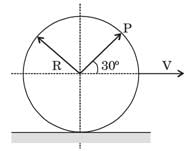
[2008]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 12

The instantaneous centre of rotation of the disk is 0, i.e. its point of contact with ground every other point on the disk is rotating with respect to this center with an angular velocity.
ω = v/R

⇒ Velocity of P = ω. OP = v/R .√3R =√3v 

Past Year Questions: Translational And Rotational Motion - Question 13
Save

A solid disk of radius r rolls without slipping on a horizontal floor with angular velocity ω and angular acceleration α. The magnitude of the acceleration of the point of contact on the disc is

[2012]
Past Year Questions: Translational And Rotational Motion - Question 14
Save

A circular solid disc of uniform thickness 20 mm, radius 200 mm and mass 20 kg, is used as a flywheel. If it rotates at 600 rpm, the kinetic energy of the flywheel, in Joules is

[2012]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 14

K.E. of fly wheel = 1/2 Iω2
where, 

= 62.83 rad/s
∴ K.E. = 1/2 × 0.4 × 62.832 = 790 J

Past Year Questions: Translational And Rotational Motion - Question 15
Save

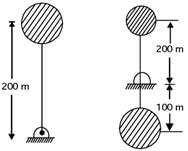
A mobile phone has a small motor with an eccentric mass used for vibrator mode. The location of the eccentric mass on motor with respect to center of gravity (CG) of the mobile and the rest of the dimension of the mobile phone are shown. The mobile is kept on a flat horizontal surface.

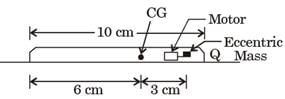
Given in addition that the eccentric mass = 2 grams, eccentricity = 2.19 mm, mass of the mobile = 90 grams, g= 9.81 m/s2. Uniform speed of the motor in RPM for which the mobile will get just lifted off the ground at the end Q is approximately

[2015]
Detailed Solution for Past Year Questions: Translational And Rotational Motion - Question 15

When lifted from ground at Q
Reaction = 0
∴ taking moments about ‘p’ and equating to 0
.09 × .06 = mr ω2 × .09
9.01 × .09 × .06 = .002 × 2.19 × 10–3 × ω2 × .09
ω = 366.50 rad/s
= 3500 rpm

Information about Past Year Questions: Translational And Rotational Motion Page
In this test you can find the Exam questions for Past Year Questions: Translational And Rotational Motion solved & explained in the simplest way possible. Besides giving Questions and answers for Past Year Questions: Translational And Rotational Motion, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

Download as PDF

Top Courses for Mechanical Engineering

Important Questions for Past Year Questions: Translational And Rotational Motion

Find all the important questions for Past Year Questions: Translational And Rotational Motion at EduRev.Get fully prepared for Past Year Questions: Translational And Rotational Motion with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Past Year Questions: Translational And Rotational Motion syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Past Year Questions: Translational And Rotational Motion resources.

Past Year Questions: Translational And Rotational Motion MCQs with Answers

Prepare for the Past Year Questions: Translational And Rotational Motion within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Past Year Questions: Translational And Rotational Motion

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Past Year Questions: Translational And Rotational Motion with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup