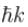Postulates Of Quantum Mechanics MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Postulates Of Quantum Mechanics MCQ Level - 2
Consider a set of wave functions ψi(x). Which of the following condition guarantees that the functions are normalized and mutually orthogonal? (i, j take values from 1 to n)
The phase velocity of ripples on a liquid surface is 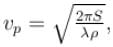 where S is the surface tension and ρ the density of the liquid. The group velocity of the ripples is given by :
where S is the surface tension and ρ the density of the liquid. The group velocity of the ripples is given by :
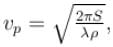 where S is the surface tension and ρ the density of the liquid. The group velocity of the ripples is given by :
where S is the surface tension and ρ the density of the liquid. The group velocity of the ripples is given by :The solutions of a free particle are :
The wave function for a particle constrained to move in 1D is shown in the graph below.

What is the probability that the particle would be found between x = 2 and x = 4 ?
The probability current density 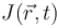 is given as
is given as 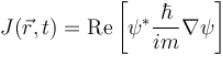 Which of the following is true?
Which of the following is true?
Smallest possible uncertainty in position of the electron moving with velocity 3 × 107 m/s. Given, h = 6.63 × 10–34 Js, m0 = 9.1 × 10–31 kg.
The wave function of the particle lies in which region?
A linear harmonic oscillator of mass m oscillates with a frequency 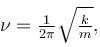 where k is its force constant. What is the minimum energy of the oscillator.
where k is its force constant. What is the minimum energy of the oscillator.
Choose the correct statement for a free particle with ψ(x) = Aeikx


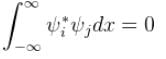
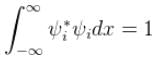
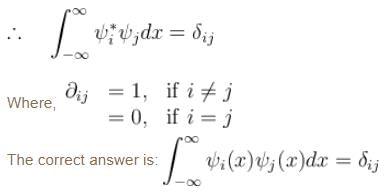

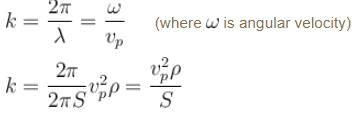
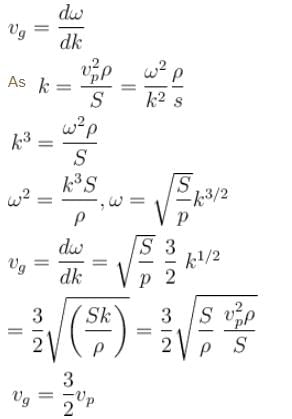
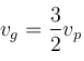

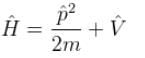

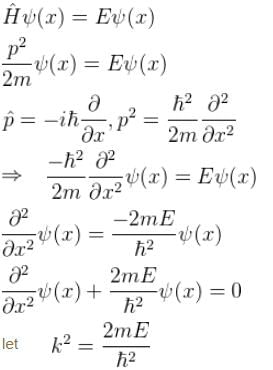
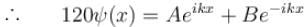 (General solution)
(General solution)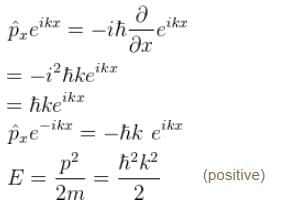
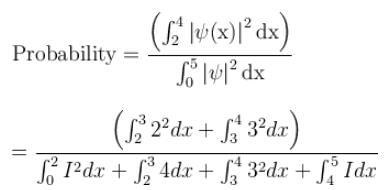
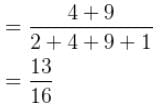
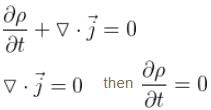
 Probability current density
Probability current density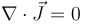 then probability density is constant in time.
then probability density is constant in time.
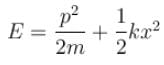

 with the square of the corresponding uncertainties.
with the square of the corresponding uncertainties.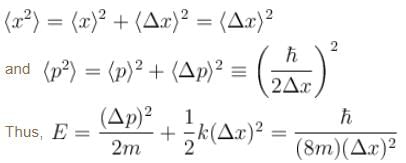
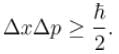 To determine the minimum energy of the oscillator, we put
To determine the minimum energy of the oscillator, we put
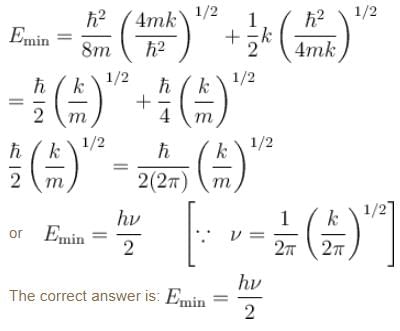
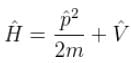
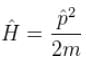


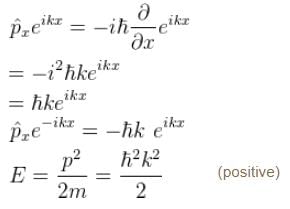
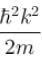 and momentum is
and momentum is