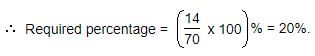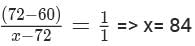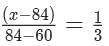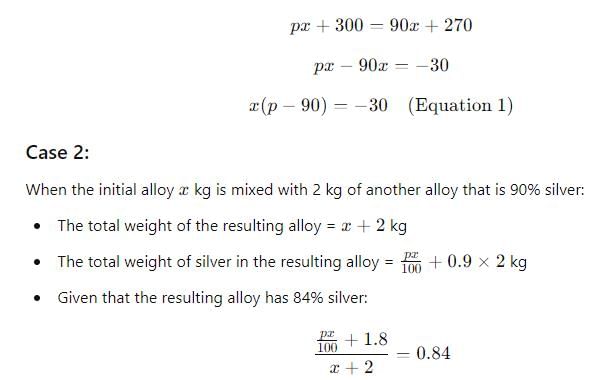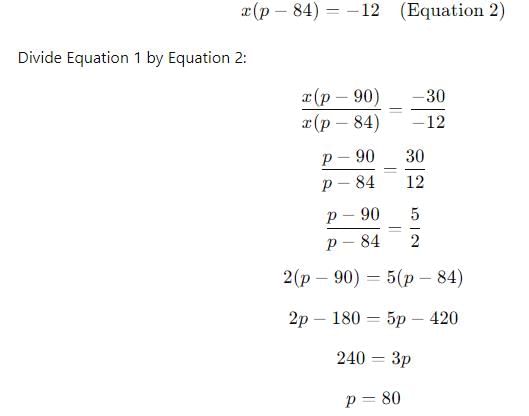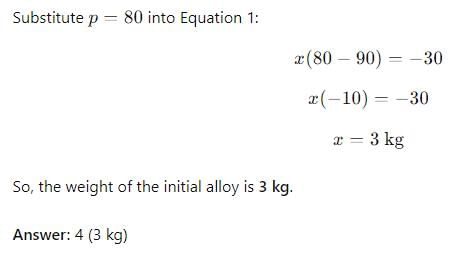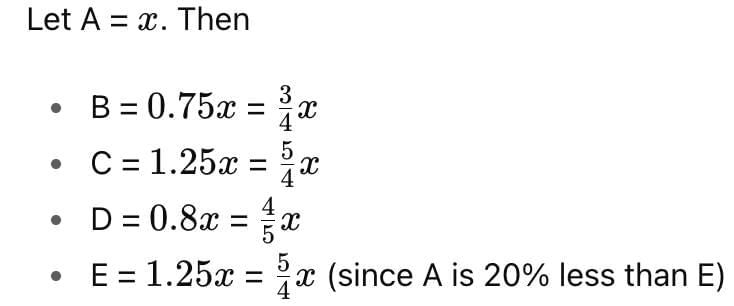Practice Test: Percentages - 2 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Practice Test: Percentages - 2
Q. Two students appeared at an examination. One of them secured 9 marks more than the other and his marks was 56% of the sum of their marks. The marks obtained by them are:
In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
What percentage of numbers from 1 to 70 have 1 or 9 in the unit's digit?
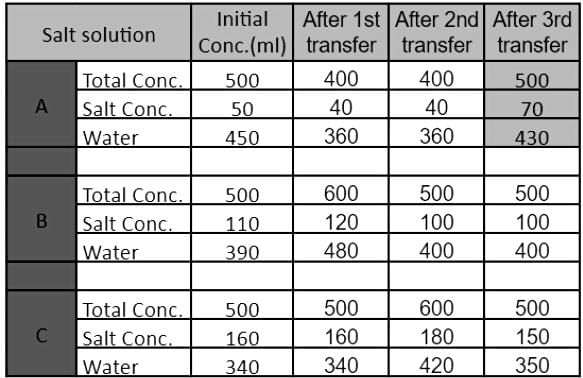
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
In an examination, the maximum possible score is N while the pass mark is 45% of N. A candidate obtains 36 marks, but falls short of the pass mark by 68%. Which one of the following is then correct?
In an election between two candidates, one got 55% of the total valid votes, 20% of the votes were invalid. If the total number of votes was 7500, the number of valid votes that the other candidate got, was:
Three candidates contested an election and received 1136, 7636 and 11628 votes respectively. What percentage of the total votes did the winning candidate get?
Two alcohol solutions, A and B, are mixed in the proportion 1:3 by volume. The volume of the mixture is then doubled by adding solution A such that the resulting mixture has 72% alcohol. If solution A has 60% alcohol, then the percentage of alcohol in solution B is
If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
B makes 25% less money than A. C is 25% better off than A. D makes 20% less money than A. A makes 20% less than E does. A, B, C, D, and E all earn whole numbers that are less than Rs.100. What is the total amount that all five of them made?
|
191 videos|213 docs|103 tests
|