Practice Test for IIFT - 9 - CAT MCQ
30 Questions MCQ Test - Practice Test for IIFT - 9
Group Question
Answer the following question based on the information given below.
The tables below show the number of total employees and number of managers for ten companies across the globe for the period 2008-2014.
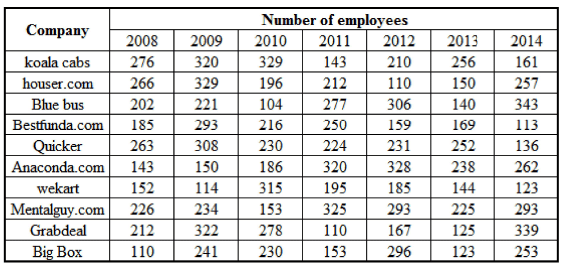
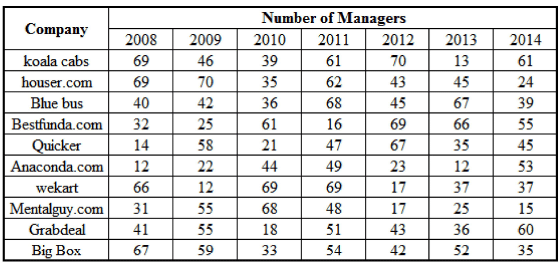
Q. What is the approximate proportion of managers to non-managers for the period 2009-2011?
The tables below show the number of total employees and number of managers for ten companies across the globe for the period 2008-2014.
The tables below show the number of total employees and number of managers for ten companies across the globe for the period 2008-2014.


Q. For which of the following companies is the proportion of managers to total employees over the entire period not less than 25%?
The tables below show the number of total employees and number of managers for ten companies across the globe for the period 2008-2014.


Q. In which of these years has the maximum number of companies shown a higher number of non-managers compared to the previous year?
The tables below show the number of total employees and number of managers for ten companies across the globe for the period 2008-2014.
Q. For how many companies is the total number of employees in the first two years less than the total number of employees in the last two years?
The tables below show the number of total employees and number of managers for ten companies across the globe for the period 2008-2014.
Q. Which of the following statements is not true?
Group Question
Answer the following question based on the information given below.
Six friends - Ajay, Bharti, Charu, Dushyant, Esha and Farhaan - are working on a research project in groups of two, as a part of their college curriculum. Their research areas include Physics, Chemistry, Mathematics and Biology. Table 1 summarizes the different research areas of all project groups, while Table 2 summarizes the marks obtained in the respective projects by each member of these very groups. Table 3 provides the maximum marks allotted to each project of a particular research area, and the number of credits awarded to each member of a group that scores above 60% in that project. A student is not awarded any credit if he/she scores 50% or less in a project and 3 credits if he/she scores between 50% and 60%. If a student drops a particular project, he/she is allowed to join another group and work on that group’s project. In such a case, he/she gets credits as per the group’s result in that new project. If a students drops a project, his/her partner can still complete the project. The number of members in a group cannot exceed 3.
Q. Which of the following project groups got the highest percentage?
Six friends - Ajay, Bharti, Charu, Dushyant, Esha and Farhaan - are working on a research project in groups of two, as a part of their college curriculum. Their research areas include Physics, Chemistry, Mathematics and Biology. Table 1 summarizes the different research areas of all project groups, while Table 2 summarizes the marks obtained in the respective projects by each member of these very groups. Table 3 provides the maximum marks allotted to each project of a particular research area, and the number of credits awarded to each member of a group that scores above 60% in that project. A student is not awarded any credit if he/she scores 50% or less in a project and 3 credits if he/she scores between 50% and 60%. If a student drops a particular project, he/she is allowed to join another group and work on that group’s project. In such a case, he/she gets credits as per the group’s result in that new project. If a students drops a project, his/her partner can still complete the project. The number of members in a group cannot exceed 3.
Q. Bharti has had to drop her Chemistry project with Dushyant (who completes it alone) due to her extra-curricular commitments. If she has joined another group but not lost credits, which of these groups has she joined?
Six friends - Ajay, Bharti, Charu, Dushyant, Esha and Farhaan - are working on a research project in groups of two, as a part of their college curriculum. Their research areas include Physics, Chemistry, Mathematics and Biology. Table 1 summarizes the different research areas of all project groups, while Table 2 summarizes the marks obtained in the respective projects by each member of these very groups. Table 3 provides the maximum marks allotted to each project of a particular research area, and the number of credits awarded to each member of a group that scores above 60% in that project. A student is not awarded any credit if he/she scores 50% or less in a project and 3 credits if he/she scores between 50% and 60%. If a student drops a particular project, he/she is allowed to join another group and work on that group’s project. In such a case, he/she gets credits as per the group’s result in that new project. If a students drops a project, his/her partner can still complete the project. The number of members in a group cannot exceed 3.
Q. If Bharti, Charu and Dushyant are allowed to join each other’s project groups but not change the number of projects they were originally working on, what is the maximum number of credits that any of them can score? Assume that a group can have any number of people for only this question.
Six friends - Ajay, Bharti, Charu, Dushyant, Esha and Farhaan - are working on a research project in groups of two, as a part of their college curriculum. Their research areas include Physics, Chemistry, Mathematics and Biology. Table 1 summarizes the different research areas of all project groups, while Table 2 summarizes the marks obtained in the respective projects by each member of these very groups. Table 3 provides the maximum marks allotted to each project of a particular research area, and the number of credits awarded to each member of a group that scores above 60% in that project. A student is not awarded any credit if he/she scores 50% or less in a project and 3 credits if he/she scores between 50% and 60%. If a student drops a particular project, he/she is allowed to join another group and work on that group’s project. In such a case, he/she gets credits as per the group’s result in that new project. If a students drops a project, his/her partner can still complete the project. The number of members in a group cannot exceed 3.
Q. Who was Ajay’s partner in the project in which Ajay scored the maximum percentage?
Six friends - Ajay, Bharti, Charu, Dushyant, Esha and Farhaan - are working on a research project in groups of two, as a part of their college curriculum. Their research areas include Physics, Chemistry, Mathematics and Biology. Table 1 summarizes the different research areas of all project groups, while Table 2 summarizes the marks obtained in the respective projects by each member of these very groups. Table 3 provides the maximum marks allotted to each project of a particular research area, and the number of credits awarded to each member of a group that scores above 60% in that project. A student is not awarded any credit if he/she scores 50% or less in a project and 3 credits if he/she scores between 50% and 60%. If a student drops a particular project, he/she is allowed to join another group and work on that group’s project. In such a case, he/she gets credits as per the group’s result in that new project. If a students drops a project, his/her partner can still complete the project. The number of members in a group cannot exceed 3.
Q. Which among the following actions helps Bharti increase her number of credits, when all projects are completed?
Group Question
Answer the following question based on the information given below.
The following charts represent the placement report of ‘School of Business’ for the academic year 2010-2011. All numbers are rounded off to the nearest integer. Each student gets exactly one offer. Answer the following questions based on the data provided in the charts.
Q. How many international offers were made in 2011-2012?
The following charts represent the placement report of ‘School of Business’ for the academic year 2010-2011. All numbers are rounded off to the nearest integer. Each student gets exactly one offer. Answer the following questions based on the data provided in the charts.
Q. The number of offers made in BFSI in 2013-2014, when compared to those made in 2011-2012, is approximately:
The following charts represent the placement report of ‘School of Business’ for the academic year 2010-2011. All numbers are rounded off to the nearest integer. Each student gets exactly one offer. Answer the following questions based on the data provided in the charts.
Q. What was the approximate number of domestic offers in IT/ITeS in 2012- 2013?
The following charts represent the placement report of ‘School of Business’ for the academic year 2010-2011. All numbers are rounded off to the nearest integer. Each student gets exactly one offer. Answer the following questions based on the data provided in the charts.
Q. What is the approximate proportion of domestic offers in FMCG as a percentage of total offers in 2013-2014?
The following charts represent the placement report of ‘School of Business’ for the academic year 2010-2011. All numbers are rounded off to the nearest integer. Each student gets exactly one offer. Answer the following questions based on the data provided in the charts.
Q. How many offers have been made in Consulting and Telecom from 2010- 2011 to 2013-2014?
Let S1 be a square of side a units. A circle C1 is inscribed in S1. Another square, S2, is inscribed inside the circle C1. Another circle, C2, is inscribed inside the square S2. Another square, S3, is inscribed inside the circle C2 and so on. Find the ratio of perimeters of all the circles to perimeters of all the squares.
The sum of an A.P of hundred terms is 1. If the sum of last 15 terms is twice the sum of first 15 terms, what is the 8th term of the A.P.?
A greedy shopkeeper first removes 50% of the pure alcohol he has and mixes an equal quantity of water in it. He then removes 50% of mixture and again mixes the same quantity of water in it. If he performs this action 5 more times, what is the percentage of alcohol remaining in the mixture?
As per a government directive, the BMC has been told to convert some part of all its swimming pools to a children’s swimming area. One of the BMC’s pools is shaped as a regular hexagon. The area designated as a children’s area is created by joining the centre of the pool to the two non-common vertices of two adjacent sides. The children’s swimming area forms what proportion of the pool now left for other swimmers?
Anil started a printing press with Rs. 26,000. After 3 months, Mukesh joined him with Rs. 16,000. After some more time, Sunil joined them with Rs. 25,000. At the end of the year, out of the total profit of Rs. 15,453, Sunil got Rs. 3,825 as his share. How many months after Mukesh did Sunil join the business?
S is the set of all possible arrangements of the word “APPLE”. Arjun picks one word randomly from this set. What is the probability that Arjun finds one P between two vowels in the chosen word?
Three vessels having volumes in the ratio of 1 : 3 : 5 are full of a mixture of water and milk. In the first vessel, ratio of water and milk is 7 : 13, in second 9 : 11 and in third 11 : 14. If the liquid in all the three vessels were mixed in a bigger container, what is the resulting ratio of water and milk?
Two trains simultaneously leave cities A and B for B and A respectively. Both trains travel at a uniform speed. They meet at a distance 500 km away from city A for the first time. The second time, they meet at a distance 400 km from city B. What is the distance between the two cities (in km)? Assume that whenever a train reaches one city, it leaves for the other city immediately.
If a = b4x, b = c2y and c = az, what is the value of xyz, for x, y, z
In an amusement park, a triangular garden is to be constructed to build a ‘zig-zag maze’. One side of the garden measures 261 m. The ratio of the length of the second and third side is 7 : 6. One of the common factors of the length of the second and the third side is an even power of 3. What is the perimeter of the garden (in m)?
The PIN number of a particular credit card has to be a three-digit number which doesn't start with 0. Santosh has forgotten his PIN number, but remembers that it is an odd number and uses some digits from 0, 1, 2, 6 and 8 exactly once. How many different values are possible for his PIN number?
Consider the Venn-diagram given below:
The pentagon, circle and square denote the number of people speaking French, German and Spanish respectively in an area. 124 people were surveyed in all. 5 people do not speak any of the given three languages. If 29 people speak French and German, how many persons speak Spanish?
A person deposits Rs. 10 Lakhs in a bank at a compounded rate of 4% per annum. He also plans to deposit Rs. 2 lakh per year in this account, starting from the end of the first year. What amount (in Rs. lakhs) will he be able to withdraw at the end of 15 years?
(Given: 1.0415 = 1.801)














