Practice Test for NMAT - 10 - CAT MCQ
30 Questions MCQ Test - Practice Test for NMAT - 10
If Disha buys 28 pens or 49 pencils or 98 erasers with the amount she has, then she is left with no money. She used 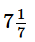 % of the money she has for travelling and bought 22 pens along with some pencils and erasers. If number of pencils she bought is more than that of erasers, then how many pencils did she buy?
% of the money she has for travelling and bought 22 pens along with some pencils and erasers. If number of pencils she bought is more than that of erasers, then how many pencils did she buy?
A certain sum of money, compounded annually, doubles itself in five years. Find the number of years it will take to quadruple itself, compounded annually and at the same interest rate?
Ram was born 12 years before Shyam. In 1976, Ram’s age was two more than thrice Shyam’s age. Ram died at the age of 48, in which year?
The students in three classes I, II and III are in the ratio of 2 : 3 : 4. If 40 students are added in each class, the ratio becomes 4 : 5 : 6. The total number of students in all the three classes is:
A line A is at a distance of 2/5 from a line 3x + 4y = 4 and passes through (-2, 3). What is the acute angle between the lines 2x + 5y + 9 = 0 and line A?
A cook visiting a mall sees 3 types of Basmati rice available i.e. costing Rs. 20 per kg, Rs. 25 per kg and Rs. 28 per kg respectively. In what ratio should he buy the three types (from the cheapest to costliest, in that order) so that his average cost comes out to Rs. 23 per kg?
The distance between stations Wasseypur and Chasseypur is 450 km. A train runs between them at a uniform speed. On a particular Thursday, in the train starting from Wasseypur, a passenger tried pulling the chain at Nosseypur with the result that it lost 80% of its speed and reached Chasseypur 50 minutes late. Had he tried doing it at Masseypur, a place 20 km away, the train would have reached 45 minutes late. How far is Masseypur from Wasseypur?
If Sam can complete 15/16th of a certain task in one day, what fraction of that task would be left if Sam works only for half a day?
What is the remainder when 123124125.........844845846 is divided by 11?
A natural number when divided by D leaves remainder 5. When four times of the number is divided with D, we get remainder as 8. Which of the following can be the value of D? (Given: D is a natural number.)
In a marriage hall, 3 lights are installed which are switched on after every 9 sec, 13 sec, 16 sec respectively. Also each light stays switched on for 1 sec. If now they switched off simultaneously then after how much time will they get switched off simultaneously again?
Consider the following statements
Q.Which of the statements is/are incorrect?
For a quadratic equation with roots x and y the sum and the product of the roots is 7 and 6 respectively. What is the sum of the roots of the quadratic equation having positive integer roots, and whose product of roots is given by x2(1 - y) + 2xy + y2( 1 - x)?
In a parallelogram ABCD, angles A, C and D measure (a + 40)°, (2a + 10)° and (b - 20)° respectively. How much does angle B measure (in degrees)?
For how many values of k do the equations x2 - y2 = 0 and (x - k)2 + y2 = 1 have exactly 3 real solutions
Which of these can be the value of y if 2sin2y + cosy - 2 = 0 ?
The largest possible sphere is inscribed in a cone of base radius 6 cm and slant height equal to the diameter of the base. What is the difference between the volume of the cone and the sphere (in cm3)?
If (x + y + z) = 6 and (xy + yz + zx) = 11, then the value of (x3 + y3 + z3 - 3xyz) is:
In how many ways can the letters of the word AIRLINES be arranged so that all the vowels are at odd positions?
Find the difference between the number of non-negative integral solutions and positive integral solutions of the equation w + x + y + z = 15
Ajay and Vijay are two incorrigible liars. Ajay lies 1 out of 4 times and Vijay lies 3 out of 5 times. If both of them make a statement each, what are the odds that they contradict each other?
What day of the week was 15 August 1947, if the first day of the calendar was Sunday?
Each question is followed by two statements, I and II. Answer each question using the following instructions:
Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements.
Q.How many cars pass through a road on day 2?
I. Average number of cars on day 1 and day 3 is 40.
II. Average number of cars on days 2, 3 and 4 is 1 less than the average number of cars on days 1, 2 and 3.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q.What is the area of ΔAEB in the quadrilateral below?
A. A (AA ED): A(ΔAEB) = 1 : 2
B. A (AB EC): A(ΔAEB) = 3 : 1
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
f(α) = aα26 + bα25 + cα24 + ... + zα. Is 1, a root of f(α)?
A . a + b + c + d + e + ... + x + y + z = o
B. a, b, c , d... y, z are all greater than 0
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q.What is the value of k?
A. k is a common positive integer root of 2x2 + px - 5 = 0 and x2 - 3x - 4 = 0
B. k2 - 2k - 8 = 0
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Sum of certain numbers is 1001 and their arithmetic mean is an integer.
Q.What is the arithmetic mean of these numbers?
A. GM of these numbers is 143.
B. All numbers are equal
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q.How many overs did Sachin and Sourav take to forge a hundred run partnership?
A. They scored 150 runs in 30 overs.
B. At the end of the partnership, Sachin’s scoring rate was thrice of Sourav's scoring rate i.e. if Sourav scored 1 run in 1 ball, Sachin scored 3 runs in one ball.
Answer the following question based on the information given below.
The following data was tabulated in a Physics lab by a student. The student was trying to find out the relation between pressure, volume and temperature of gas under controlled conditions in order to understand the behaviour of the gas.
Q.In the above experiment the volume of gas has increased from |0west va|Ue to the highest value by what percentage?
The following data was tabulated in a Physics lab by a student. The student was trying to find out the relation between pressure, volume and temperature of gas under controlled conditions in order to understand the behaviour of the gas.
Q.The experiment has been used to prove that PV = kT, where, P: Pressure, V: Volume, T: Temperature, and k: some constant. Which reading is an exception to this?














