Practice Test for NMAT - 13 - CAT MCQ
30 Questions MCQ Test - Practice Test for NMAT - 13
Answer the following question based on the information given below.
The graph below gives details of total exports as well as exports of herbal products for a company.
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.
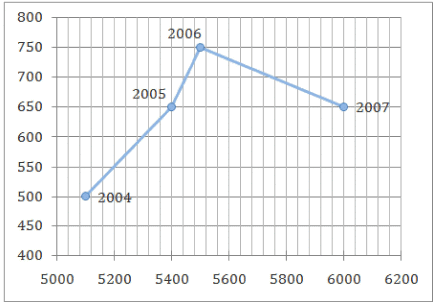
Q.For 2006, herbal products formed what percentage of the total exports?
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.
The graph below gives details of total exports as well as exports of herbal products for a company.
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.

Q.The fall in herbal exports in 2007 from that in 2006 was nearly:
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.
The graph below gives details of total exports as well as exports of herbal products for a company.
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.

Q.Over the given period, the herbal exports rose by nearly:
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.
The graph below gives details of total exports as well as exports of herbal products for a company.
The abscissa represents the total exports for a given year in Rs. Lakhs, while the ordinate represents the exports of herbal products for that same year in Rs. Lakhs.
Q.The average percentage increase in total exports was:
The ratio of cost price and marked price of an article is 2 : 3. The ratio of percentage profit and percentage discount is 3 : 2. What is the discount percentage?
Jai and Veeru are two masons who are given the job of building a compound wall around a plot owned by Mr. Thakur. Jai working alone takes 8 hours more than the time that both Jai and Veeru would take working together. Veeru working alone takes 12.5 hours more than the time that both would take working together. How many hours would Jai alone take to build the wall?
where a, b and c are in continued proportion and b, c and a are in continued proportion.
A number which reads the same when read forward and backward is called a palindrome.
Q.How many four-digit numbers are palindromes?
The sum of a two-digit number and the number formed by interchanging the two digits is 45 more than twice the original number. If the sum of the digits of the number is 9, what is the original number?
Group Question
Answer the following question based on the information given below.
A company with pan-India presence has segregated its operations into four regions - North, East, West and South. For tracking purposes, each region is further divided into two sub-regions i.e. 1 and 2. e.g. North is divided into North 1 and North 2, and so on. The bar-graph below shows the percentage distribution of male and female employees of the company in these eight sub-regions.
The percentage of male employees in the North, West, South, and East regions is 60%, 55%, 30% and 45% respectively.
Q.The ratio of total employees in North 1 to North 2 is
A company with pan-India presence has segregated its operations into four regions - North, East, West and South. For tracking purposes, each region is further divided into two sub-regions i.e. 1 and 2. e.g. North is divided into North 1 and North 2, and so on. The bar-graph below shows the percentage distribution of male and female employees of the company in these eight sub-regions.
Q.If there are 500 employees in West, how many male employees does West 2 have?
A company with pan-India presence has segregated its operations into four regions - North, East, West and South. For tracking purposes, each region is further divided into two sub-regions i.e. 1 and 2. e.g. North is divided into North 1 and North 2, and so on. The bar-graph below shows the percentage distribution of male and female employees of the company in these eight sub-regions.
Q.If there are 60 male employees in South 2, what is the total number of employees in South?
A company with pan-India presence has segregated its operations into four regions - North, East, West and South. For tracking purposes, each region is further divided into two sub-regions i.e. 1 and 2. e.g. North is divided into Northl 1 and North 2, and so on. The bar-graph below shows the percentage distribution of male and female employees of the company in these eight sub-regions.
Q.The ratio of female employees in East 1 to East 2 is
Group Question
Study the table given below and answer the questions that follow:
The table below shows the cours-wise and section-wise breakup of students in a university.
Q.If all the boys and 80% of all the girls are successful in the courses taken by them, what is the combined passing percentage of the university?
The table below shows the cours-wise and section-wise breakup of students in a university.
Q.In which course is the number of girls as a percentage of the total students in that course the highest?
The table below shows the cours-wise and section-wise breakup of students in a university.
Q.By what percentage is the number of students pursuing a course in Computers more than the number of students pursuing Finance?
The table below shows the cours-wise and section-wise breakup of students in a university.
Q.The number of successful students in the Computers course is thrice the number of successful girl students in the Business Management course. If the number of successful girl students in the Business Management course is 46% of all the girls in this course, what is the percentage of successful students in the Computers course?
D, E, F are the mid points of the sides BC, CA and AB respectively of a triangle ABC. What is the ratio of the circumradii of triangles DEF and ABC respectively?
In a plane there are two lines, a and b. a has 4 points on it while b has 5 points on it. Beside this there are six other points in this plane, no three of which are collinear. Also, apart from the points that lie on lines a and b, no three points are collinear. What is the maximum number of quadrilaterals that can be drawn using these points?
Raman gives Suman a head start of 35 m in a 200 m race but still beats Suman by 45 m. In a 100 m race, both start simultaneously from the same point. By how many metres does Raman beat Suman in the 100 m race?
Two friends, A and B, decide to play a game. Each friend has the same probability of winning a single game i.e. p. If the amount at stake is Rs. 22, and A is expected to win Rs. 12 if he starts first, what is the value of p ?
A circular wire of area 4π sq.cm is bent into a square. The area of the square is what percentage of the area of the circle?
The average of a, b and c is 113. What is the value of b, if c is as much more than the average as much as a is less than the average?
A piece of work when done by Amar, Akbar and Anthony respectively, costs Rs. 540, Rs.324 and Rs. 320 respectively. The daily wages of Amar, Akbar and Anthony are Rs.36, Rs.18 and Rs.32 respectively. What will be the total cost when Amar, Akbar and Anthony are working together?
Five circles, each of radius 6 cm, are cut-out from a circular sheet of radius 14 cm. What is the ratio of the area of the remaining portion of the sheet to the area of the original sheet?
Each question is followed by two quantities, A and B. Answer each question using the following instructions:
Mark (1) if quantity A is greater than quantity B.
Mark (2) if quantity B is greater than quantity A.
Mark (3) if the two quantities are equal.
Mark (4) if it is impossible to determine a relationship.
Mark (5) if the greater quantity cannot be determined but the two quantities are definitely not equal.
In oodoo-dudu Island, coins are available only in two denominations - 4 Rupee and 5 Rupee. Rajesh had paid an amount of Rs. 150 to the shopkeeper.
A. The probability that the number of 4 rupee coins given by Rajesh is more than the number of 5 rupee coins.
B. The probability that the number of 5 rupee coins given by Rajesh is more than the number of 4 rupee coins.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q.Two quadratic equations 2x2 - 7x + k = 0 and x2 + x - 6 = 0 have a common root. What is the value of k?
A. k is a positive integer.
B. k + 39 is a natural number
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q.A factory has two different units - A and B. For the past twelve days, two new workers joined the factory daily, in two different units respectively (one in each of the two units). Is the number of workers in Unit A more than the number of workers in Unit B?
A. Five days ago, number of workers in Unit A was twice the number of workers in Unit B.
B. Ten days ago, number of workers in Unit B was thrice the number of workers in Unit A.




















