Practice Test for NMAT - 9 - CAT MCQ
30 Questions MCQ Test Mock Test Series for NMAT - Practice Test for NMAT - 9
Three jugs of equal volume contain juice and water in the ratio of 3 : 2, 5 : 4 and 1 : 4 respectively. If all three jugs are full and then their solutions are mixed, what is the ratio of juice to water in the resultant mixture?
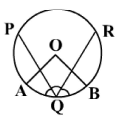
In the above circle with centre O, PQ and QR are equal chords. OA and OB bisect the chords PQ and QR respectively. If 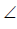 PQR = 40°, what is the value of
PQR = 40°, what is the value of 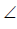 ACB? C is a point on the circle, lying on major arc AB.
ACB? C is a point on the circle, lying on major arc AB.
The goods in a godown are to be moved to a different location. 20 men can move all the goods in 185 days. 20 men start the work and 10 additional men are deployed after every 20 days. How long do the goods actually take to get transferred?
Group Question
Answer the following question based on the information given below.
The pie chart below shows the product-wise break-up of sales (by volume) for a company in the year 2013.
Total sales volume = 400000 units. The ratio of the selling price per unit for each product w.r.t T is as shown in the following line graph.
Q. The revenue obtained from which among the following products is the highest?
The pie chart below shows the product-wise break-up of sales (by volume) for a company in the year 2013.
Total sales volume = 400000 units. The ratio of the selling price per unit for each product w.r.t T is as shown in the following line graph.
Q. If the company earns Rs. 1.05 crores by selling product R, what is the sum (in Rs.) of the per unit selling price of products S, U and V?
The pie chart below shows the product-wise break-up of sales (by volume) for a company in the year 2013.
Total sales volume = 400000 units. The ratio of the selling price per unit for each product w.r.t T is as shown in the following line graph.
Q. Within the company, by what percentage does the revenue share of the highest selling product (by revenue) exceed that of its nearest competitor?
The pie chart below shows the product-wise break-up of sales (by volume) for a company in the year 2013.
Total sales volume = 400000 units. The ratio of the selling price per unit for each product w.r.t T is as shown in the following line graph.
Q. If the pie-chart drawn for sales volume is redrawn excluding S, what percent of the total sales by volume would be due to product T?
The pie chart below shows the product-wise break-up of sales (by volume) for a company in the year 2013.
Total sales volume = 400000 units. The ratio of the selling price per unit for each product w.r.t T is as shown in the following line graph.
Q. If a light flashes every 18 seconds, how many times it will flash in three-fourths of an hour? Assume that the first flash was just as the hour began.
In a college, the average age of 10 male teachers, 7 female teachers and 1 student is 46 years. If the average age of the male teachers is 47 years and that of the female teachers is 48 years, then what is the age of the student?
Bag A contains 9 white and 5 green balls. Bag B contains 6 white and 7 green balls. One ball is drawn at random from bag A and is placed in bag B. Now one ball is drawn at random from bag B. Given that the ball picked from bag B is green, what is the probability that a white ball was transferred from bag A?
The remainder of 13571357... upto nine hundred digits, when divided by 9999 is?
The largest number by which the expression n3 - n is divisible, for all integral values of n such that n > 1, is:
What is the number of 10-digit numbers divisible by 8 that can be formed using only the digits 2, 3 and 5?
If log0.1(x2 - 8x + 17) < log0.1(3x - 7), find the range of x.
Group Question
Answer the following question based on the information given below.
The table below shows the foreign direct investment (FDI) flowing out of each country as a percentage of its GDP.
The table below shows the total FDI and FDI through Singapore received by China and India. All figures in that table are in billion dollars.
Q. From 1995 to 2003, which of the given countries showed the highest percentage increase in FDI flowing out of that country?
The table below shows the foreign direct investment (FDI) flowing out of each country as a percentage of its GDP.
The table below shows the total FDI and FDI through Singapore received by China and India. All figures in that table are in billion dollars.
Q. If Singapore’s GDP in 2003 was four times its value in 1995, what can be said about Singapore’s FDI investement in India from 1995 to 2003, as a percentage of its total FDI outflow for those years?
The table below shows the foreign direct investment (FDI) flowing out of each country as a percentage of its GDP.
The table below shows the total FDI and FDI through Singapore received by China and India. All figures in that table are in billion dollars.
Q. If Singapore’s GDP in 2002 was $82 billion, India and China together accounted for what percentage of Singapore’s total FDI outflow?
The table below shows the foreign direct investment (FDI) flowing out of each country as a percentage of its GDP.
The table below shows the total FDI and FDI through Singapore received by China and India. All figures in that table are in billion dollars.
Q. If the FDI outflow of the United States in 2001 is $93.1 billion, what is the approximate ratio of the GDP of the United States in 2001 to that of India’s and China’s cumulative FDI in 2001?
Group Question
Answer the following question based on the information given below.
The graph below shows the number of men, women and children in a certain village over the period 2007-08 to 2013-14.
Men and women are ‘adults’ i.e. people whose age is greater than 18 years at the given time. All values are multiples of 10.
Q. In 2011-12, every fourth man and every fifth woman was aged above 45 years. What percentage of the total population of the village was aged less than 45 years?
The graph below shows the number of men, women and children in a certain village over the period 2007-08 to 2013-14.
Men and women are ‘adults’ i.e. people whose age is greater than 18 years at the given time. All values are multiples of 10.
Q. What was the highest ever annual percentage change in the population of the village?
The graph below shows the number of men, women and children in a certain village over the period 2007-08 to 2013-14.
Men and women are ‘adults’ i.e. people whose age is greater than 18 years at the given time. All values are multiples of 10.
Q. Under a scheme, the government provides medical funds to families in the village. A family comprising a man, woman and two children is categorized as a Class A family while a family comprising only a man and woman is categorized as a Class B family. Class B and Class A families respectively get Rs. 2,000 and Rs. 3,000 per month as medical funds. By what percent should the government increase its maximum budget for medical funds for 2012-13 as compared to 2009-10. Assume that the government budgets an amount exactly equal to its maximum possible outlay.
The graph below shows the number of men, women and children in a certain village over the period 2007-08 to 2013-14.
Men and women are ‘adults’ i.e. people whose age is greater than 18 years at the given time. All values are multiples of 10.
Q. 2% of the total population of the village in 2013-14 comprised adult migrants from a neighbouring village. There was no child migration to or from this village. What was the number of child births in this village from 2012-13 to 2013-14, if there was no child mortality during the given period?
When the length of a rectangle A is reduced by 4 cm, while keeping the area constant, rectangle B is formed. The breadth of B is 12 cm. If the length of B is increased by 6 cm, again keeping the area constant, rectangle C is formed and its breadth is 4 cm less than that of B. What is the area of each rectangle?
A sum of Rs. 1,450 is lent at the beginning of a year at a certain rate of interest. After 8 months, another sum of Rs. 725 is lent but at a rate that is twice the former. At the end of the year, Rs. 67 is earned as interest from both the loans. What was the original rate of interest?
Each question is followed by two statements, I and II. Select appropriate option from the given below.
What is the minimum passing percentage in a test?
I. Abhiram scored 152 marks in a test and failed by 98 marks.
II. The maximum marks of the test are 448 more than what Abhiram has scored.
Each question is followed by two statements, I and II. Select appropriate option from the given below.
What is the area of the right angled triangle?
I. The length of hypotenuse is 5 cm.
II. The perimeter of the triangle is four times its base.
Each question is followed by two statements, I and II. Select appropriate option from the given below.
What is the speed of a 280 m long train?
I. The train crosses another train, of 320 metres length and running in the opposite direction, in 27 seconds.
II. The train crosses another train, running in the same direction at the speed of 42 km/hr, in 35 seconds.
Each question is followed by two statements, I and II. Select appropriate option from the given below.
C1 and C2 are concentric circles. What is the area of the shaded region?
I. Radius of C1 = 12 cm
II. Radius of C1/Radius of C2 = 1/2
Each question is followed by two statements, I and II. Select appropriate option from the given below.
What is the first term of the series?
I. The series is an A.P. with 2 terms.
II. The series is a G.P. with 7 terms and middle term as 54.
Each question is followed by two statements, I and II. Select appropriate option from the given below.
What time is it?
I. 1 < y 9 and the minute hand is ahead of the hour hand.
II. 1 y
4 and the angle between minute hand and hour hand is 30°.
|
1 docs|29 tests
|




















