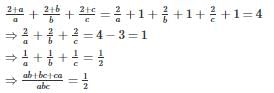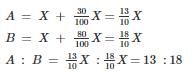Practice Test: Quantitative Aptitude - 2 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2025 - Practice Test: Quantitative Aptitude - 2
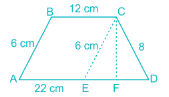
Find the approximate area of a trapezium whose parallel sides are 22 cm, 12 cm and the other sides are 8 cm and 6 cm.
A, B and C enter into a partnership, investing Rs. 6000. A invests Rs. 1000 and B and C invests in the ratio of 2 : 3. Find the profit of C, when the annual profit is Rs. 2400
A train 150 metres long crosses a pole in 15 seconds and crosses another train of the same length travelling in the opposite direction in 12 seconds. The speed of the second train in km/hr is
Trish and Stacy can complete a work in 20 days and 30 days, respectively, when working alone. In an arrangement, Trish works for 2 days, and then Stacy works for a day. They keep on repeating this process till the work gets completed. On which day will the work gets completed?
If the sum of the measures of all the interior angles of polygon is 1080°, find the number of sides of the polygon?
If 2cosec2A = x, then find the value of x?
In an examination, 35% of total students failed in Hindi, 45% failed in English and 20% failed in both. Find the percentage of those students who passed in both the subjects?
A sum of Rs. 3000 amounts to Rs. 6000 in two years at compound interest. The interest for four years is
If the diagonals of a rhombus are 24 and 10, then the value of thrice its side is
If the measures of the angles of a triangle are in the ratio. 1 ∶ 2 ∶ 3 and if the length of the smallest side of the triangle is 10 cm, then the length of the longest side is
Two numbers are respectively 30% and 80% more than a third number. Find the ratio of these numbers.
A cricketer has a certain average of runs for his 6 innings. In the seventh inning he scores 100 runs, thereby increasing his average by 7 runs. His new average of runs is
If a3 - b3 = 56 and a - b = 2 then what is the value of a2 + b2?
In ΔABC, ∠B = 5∠C and ∠A = 3∠C, then the measure of ∠C is
A pole stands vertically, inside a scalene triangular park ABC. If the angle of elevation of top of the pole from each corner of the park is same, then in Δ ABC, the foot of the pole is at the
Three sides of a triangle are 5 cm, 9 cm and x cm. The minimum integral value of x is
The length of a chord which is at a distance of 5cm from the centre of a circle of radius 13cm is
Divide 43 into two parts so that 4 times the first and 3 times the second together equals to 150. Then ratio of the first and second parts is
25% discount is already offered on an item. By applying a promo code the customer wins 20% cash back. What is the effective discount?
Refer the below data table and answer the following Question :
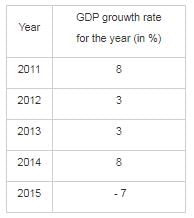
If the GDP of the country was $3 trillion at the end of 2013, what was it at the beginning of 2015?
Refer the below data table and answer the following Question :
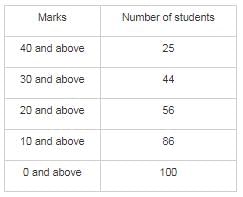
Q. Find the number of students whose marks are between 30 and 40 ?
Direction: Study the following graph and answer the question
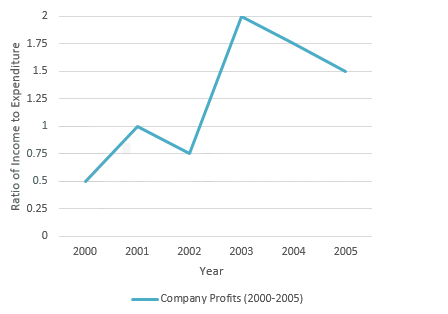
Q. If the profit made in the year 2003 was Rs. 450000, then find the income
Direction: Study the following graph and answer the question

Q. Find the percentage increase in income from 2002 to 2003
|
274 docs|133 tests
|



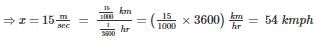

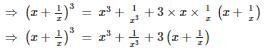 But we know that x3 + 1/x3 = 0
But we know that x3 + 1/x3 = 0
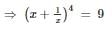



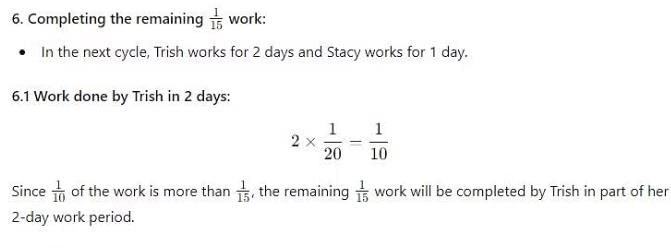

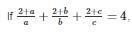 then the value of (ab + bc + ca)/abc is
then the value of (ab + bc + ca)/abc is