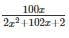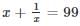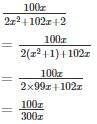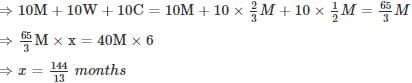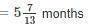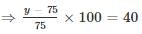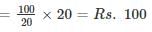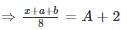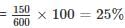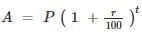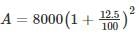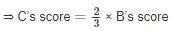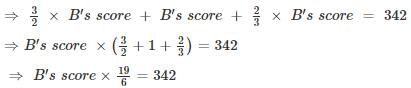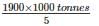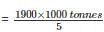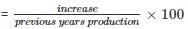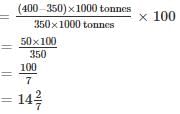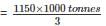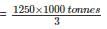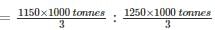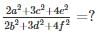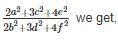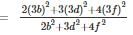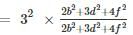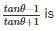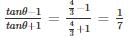Practice Test: Quantitative Aptitude - 9 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2025 - Practice Test: Quantitative Aptitude - 9
Find the value of K for which the points A (4, 3), B(5, 4) and C(K, 6) are collinear.
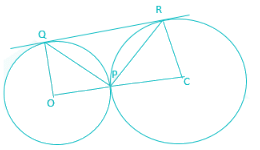
Two circles touch each other externally at P. QR is a common tangent to the circles touching them at Q and R. The measure of ∠QPR is
The difference between interior and exterior angle of a regular polygon is 100°. Find the number of sides of polygon.
A bicycle wheel makes 5000 revolutions in moving 11 km. The diameter of the wheel, in cm, is
If 40 men or 60 women or 80 children can do a piece of work in 6 months, then 10 men, 10 women and 10 children together do half of the work in
A boat goes 10kms an hour in still water, but takes twice as much time in going the same distance against the current. The speed of the current (in km/hr) is –
A shopkeeper sells a pair of sunglasses at a profit of 25%. If he had bought it at 25% less and sold it for Rs. 20 less, then he would have gained 40%. The cost price of the pair of sunglasses is:
The average age of 8 persons in a committee is increased by 2 years when two men whose ages are 35 years and 45 years are replaced by two new men. The average age of the two new men is (in years)
Two numbers are less than the third number by 20% and 28% respectively. By what per cent is the second number less than the first number?
In an examination, a student gets 20% of total marks and fails by 30 marks. Another student gets 32% of total marks which is more than the minimum pass marks by 42 marks. The pass percentage is
There is 100% increase to an amount in 8 years, at simple interest. Find the compound interest of Rs. 8000 after 2 years at the same rate of interest.
Three students A, B and C play cricket. The runs scored by A and B respectively are in the ratio 3 : 2. B’s runs to C’s runs are also in the same ratio. Together they score 342 runs. Then the runs scored by B are
Direction: The following graph shows the production of wheat flour (in 1000 tonnes) by three companies X, Y and Z over the years. Study the graph and answer the questions.
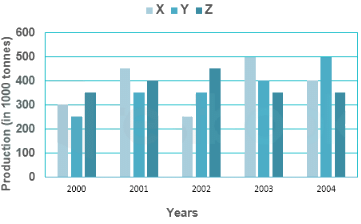
Q. The average production for five years was maximum for which company(s)?
Direction: The following graph shows the production of wheat flour (in 1000 tonnes) by three companies X, Y and Z over the years. Study the graph and answer the questions.
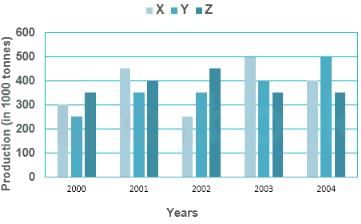
Q. What is the percentage increase in the production of company Y from 2002 to 2003?
Direction: The following graph shows the production of wheat flour (in 1000 tonnes) by three companies X, Y and Z over the years. Study the graph and answer the questions.
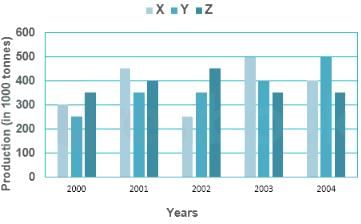
Q. What is the ratio of the average production of company X in the period 2002-2004 to the average production of company Y in the same period?
Direction: The following graph shows the production of wheat flour (in 1000 tonnes) by three companies X, Y and Z over the years. Study the graph and answer the questions.
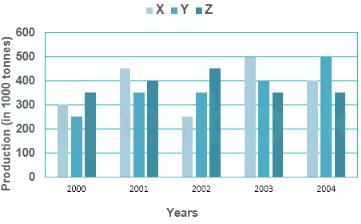
Q. What is the difference between the production of company Z in 2004 and company Y in 2000 (in thousand tonnes)?
For what value of x is (x + 3264 × 3266) a perfect square,
Which one of the following three digit numbers divides 9238 and 7091 with the same remainder in each case?
The list price of a digital electronic watch is Rs. 1000. A customer gets two successive discounts on the list price, the 1st being of 15%. Calculate the 2nd discount, if the customer pays Rs. 697 for it.
At an instant, the length of the shadow of a pole is √3 times the height of the pole. The angle of elevation of the Sun at that moment is
If for some angle θ, 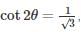 then the value of sin 3θ, where 2θ ≤ 90° is
then the value of sin 3θ, where 2θ ≤ 90° is
|
273 docs|133 tests
|


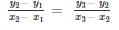
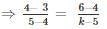

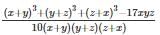
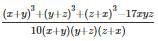
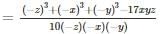
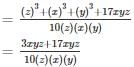
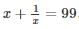 find the value of
find the value of