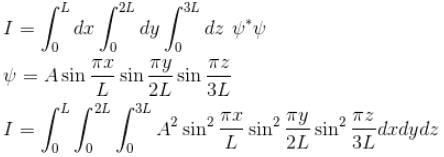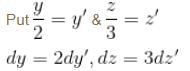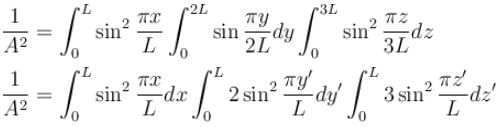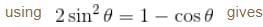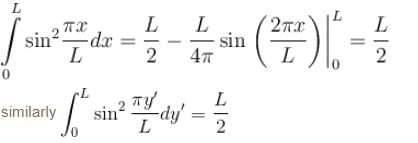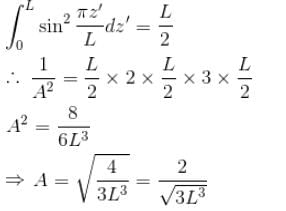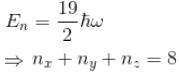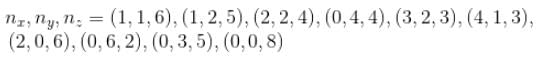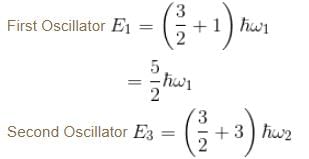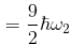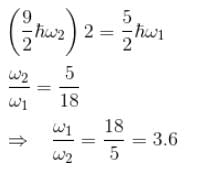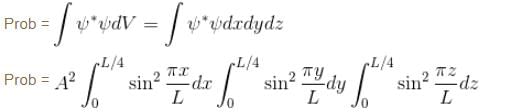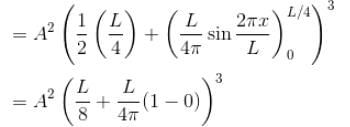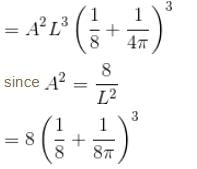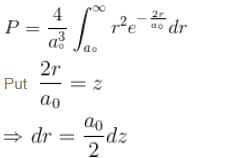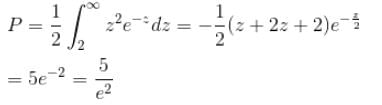Quantum Mechanics In Three Dimensions NAT - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Quantum Mechanics In Three Dimensions NAT
A stone with mass 1kg is whirled in a horizontal circle of radius 1m with a period of revolution equal to 1s. What value of orbital angular momentum quantum no. l describes this motion? (in 1034)
Calculate the minimum value of for the stone mentioned in problem 1.
Calculate the average distance of an electron from the nucleus in the ground state of hydrogen atom is unit of a0.
Find the level of degeneracy for particle in a 3d box with energy 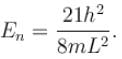
Find the value of the normalisation constant in the unit 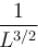 of that normalizes the ground state wavefunction of the particle in a box of lengths L, 2L, 3L in x, y and z directions respectively. Take √3 = 1.732
of that normalizes the ground state wavefunction of the particle in a box of lengths L, 2L, 3L in x, y and z directions respectively. Take √3 = 1.732
Find the level of degeneracy for a 3 dimensional isotropic quantum harmonic oscillator of energy 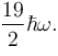
Consider two harmonic oscillators in 3 dimensions. For what ratio of angular frequencies will the first excited state of one oscillator have energy twice that of the second oscillator’s third excited state energy i.e find 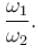
Modeling a defect trap in a crystal as a 3d box with edge length 5Å, find the values of energy for an electron bound to the defect site, assuming the electron to be in the ground state. (in eV)
Find the probability of finding a particle in a 3d box of length L, in the volume 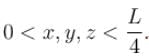
(Assume the particle to be in the ground state).
Calculate the probability that the electron in the ground state of hydrogen will be found outside the first Bohr radius in the unit e–2. Take
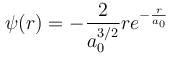


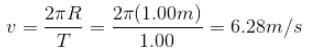
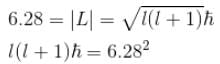
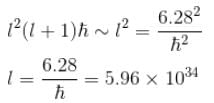


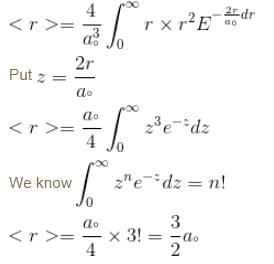
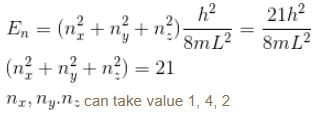
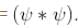 Integration over the volume of the cube must be unity
Integration over the volume of the cube must be unity