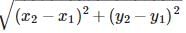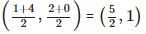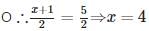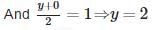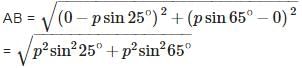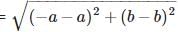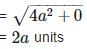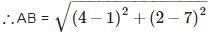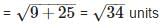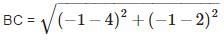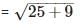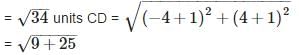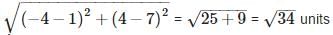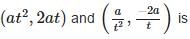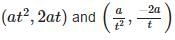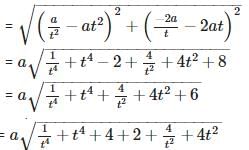RD Sharma Test: Coordinate Geometry - Grade 10 MCQ
25 Questions MCQ Test - RD Sharma Test: Coordinate Geometry
The distance of the point (– 3, 4) from the origin is
If A and B are the points (– 6, 7) and (– 1, – 5) respectively, then the distance 2AB is equal to 26 units 13 units 15 units 20 units 2AB 
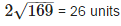
The distance between the points (a, a) and (−√3a,√3a) is
Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). The co – ordinates of the fourth vertex D are
If (a, 0) , (0, b) and (x, y) are collinear, then
The distance between the points (– 1, – 5) and (– 6, 7) is
If P(x, y) is any point on the line joining the points A(a, 0) and B(0, b), then
The distance between the points A(p sin 25∘, 0) and B(0, p sin 65∘) is
The length of the median through A of ΔABC with vertices A(7, – 3), B(5, 3) and C(3, – 1) is
If the co – ordinates of a point are (3, – 7), then its ordinate is
The distance between the points (a, b) and (– a, b) is
The vertices of a quadrilateral are (1, 7), (4, 2), (– 1, – 1) and (– 4, 4). The quadrilateral is a
If the line segment joining the points A(x1,y1) and B(x2,y2) is divided by a point P in the ratio 1 : k internally, then the co – ordinates of the point P are
If the co – ordinates of a point are (– 5, 11), then its abscissa is
If the distance between the points (p, – 5) and (2, 7) is 13 units, then the value of ‘p’ is
If A is point on the x – axis whose abscissa is 5 and B is the point (1, – 3), then the distance AB is
The point where the medians of a triangle meet is called the ________ of the triangle
The base of an equilateral triangle ABC lies on the y – axis. The co – ordinates of the point C is (0, – 3). If origin is the midpoint of BC, then the co – ordinates of B are
The values of ‘y’ for which the distance between the points (2, – 3) and (10, y) is 10 units is
The distance of the point (– 5, 12) from the y – axis is
The co – ordinates of the mid – point of the line segment joining the points (– 2, 3) and (4, – 5) are
The point where the perpendicular bisector of the line segment joining the points A(2, 5) and B(4, 7) cuts is:
The distance of a point from the y – axis is called