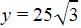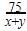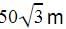RD Sharma Test: Introduction to Trigonometry - Class 10 MCQ
25 Questions MCQ Test - RD Sharma Test: Introduction to Trigonometry
In ΔABC, ∠B = 90°. If AB = 14 cm and AC = 50 cm then tan A equals :
In sin 3θ = cos (θ – 26°), where 3θ and (θ – 26°) are acute angles, then value of θ is :
If angle A is acute and cos A = 8/17 then cot A is :
The value of 2 tan2 60° – 4 cos2 45° – 3 sec2 30° is :
The value of 3/4 tan2 30° – 3 sin2 60° + cosec2 45° is
The solution of the trigonometric equation
In sin 3θ = cos (θ – 26°), where 3θ and (θ – 26°) are acute angles, then value of θ is :
The value of sin2 15° + sin2 30° + sin2 45° + sin2 60° + sin2 75° is :
The values of x and y which make the following solutions true are: cos x° = sin 52° and cos y° = sin (y° + 10)
If α + β = 90° and α = 2β then cos2 α + sin2 β equal :
A flagstaff 6 metres high throws a shadow 2 √3 metres long on the ground. The angle of elevation is :
An observer √3 m tall is 3 m away from the pole 2 √3 m high. The angle of elevation of the top from the pole is :
An observer 1.5 m tall is 28.5 m away from.a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. The height of the chimney is :
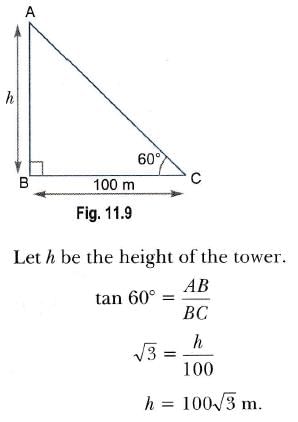
The angle of elevation of the top of a tower from a distance 100 m from its foot is 60°. The height of the tower is :
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. The length of the string is:
A tree is broken by the wind. Its top struck the ground at an angle 30° at a distance of 30 m from its foot. The whole height of the tree is :
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks then the width of the river is :
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is:
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angles of elevation from his eyes to the top of the building increases from 30 to 60° as he walks towards the building. The distance he walked towards the building is :
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 60°. If one strip is exactly behind the other on the same side of the light-house then the distance between the two ships is :
In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. The value of tan C is:
Which of the following identities is correct?




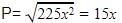
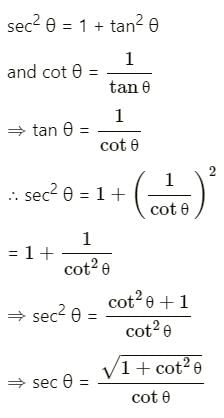

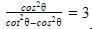
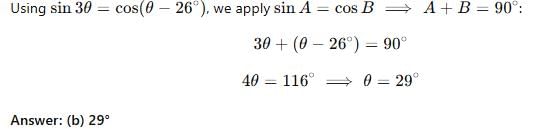
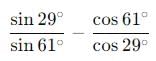 is :
is :