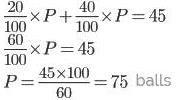RRB JE ME (CBT I) Mock Test- 10 - Mechanical Engineering MCQ
30 Questions MCQ Test - RRB JE ME (CBT I) Mock Test- 10
Find the HCF of (29 x 36 - 12 x 22) and the average of three numbers 827, 157, and 528.
Sum of three numbers is 54, and the first number is 10 more than the third and 10 less than the second number. Find the second number.
Which of the following is irrational?
a = (2√2 - 3√3)16
b = √1764 + 2√1089
c = √(14 x 59 - 67 x 3)
d = √(24 x 22 + 16 x 31)
A Faulty watch gains 5 seconds in 5 minutes. It was set right at 8 a.m. If, later that day, it shows 11:15 p.m. in the watch, what is the actual time?
The population of a village in 2016 is 2000 and it increases by 20% every year from the previous year. What is the population gained during 2018-2019?
If 40% of a is equal to two times the value of b, find a: b.
Aman invested Rs.16000 for 4 years at a 15% simple rate of interest. After 4 years, total amount received he invested for 2 years at 20% compound rate of interest. With the amount received after 2 years, he purchased an article and sold this article at Rs.40000, then what is the profit received by him after selling the article?
Given below are the steps involved. Arrange them in sequential order.
(A) Total amount after 4 years when invested at 15% SI = 16000 + [(16000 * 15 * 4)/100] = Rs.25600
(B) Cost price of article = Rs.36864 and selling price = Rs.40000
(C) Profit amount earned = 40000 - 36864 = Rs.3136
(D) Total amount after 2 years when invested at 20% CI = 25600 * (1.2)2 = Rs.36864
A car crosses a man walking at 6 km/hr. The man can see things up to 450 m, only in one direction due to fog. He sees the car, which was going in the same direction for 4.5 min. What is the speed of the car?
The ratio of the speeds of 3 Bikers is 6:4:1, and the ratio of the time for which they have travelled is 2:1:4. If the sum of the distance travelled by all of them is 60 km, what is the difference between the distance travelled by the slowest Biker and the fastest Biker?
Five children are born to Riya each at a gap of 3 years such that the age of eldest child seven years later if doubled becomes 3 less than Riya's present age. 15 years hence, the average of the three youngest children becomes 23 less than Riya's age 3 years ago. Find the age of Riya and the age of the youngest child, respectively.
In an election, there are five candidates and, each got the different number of votes. P gets more votes than U, who gets less votes than R. T receives more votes than S, who gets less votes than P. P didn't get more votes than both T and R. U didn't gets the lowest number of votes and R didn't gets the highest number of votes.
How many candidates get more votes than S, but less votes than R?
The difference between CI and SI on a certain sum of money at 20% per annum for 2 years is Rs 800, what would be the difference of CI and SI on that same sum of money after 3 years if the rate of interest was 10%?
2 men and 3 women can do a piece of work in 10 days while 3 men and 2 women can do the same work in 8 days. In how many days can 2 men and 1 woman do the work?
In a bag 40% of balls are red, 20% balls are blue and the remaining are green color balls. If the number of green and blue balls is 45, then find the number of red balls in the bag.
Prices of 10 items are given below in Rupees. Find the difference between their mean and median.
15, 5, 8, 10, 22, 25, 12, 30, 20, 18
A cloth trader gets a profit equal to selling price of 12 metres of cloth when he sells 36 metres of cloth. Find the profit percentage.
A number when divided by 3, 5 and 7 leaves remainder 2 in each case, what will be the remainder when the same number is divided by 9?
The number of pupils of a class is 1342. The ratio of the number of boy pupils to the number of girl pupils is 5: 6. If 120 boys pupils leave the class and 80 new girl pupils joined the class, then new ratio becomes:
In a Village, there are 10800 people. The %literacy is 55% and the % Female literacy is 48%. If there are 1620 more literate Males than literate Females, what is the Gender ratio(Male : Female) of the Village?
The ratio of three numbers is 3:4:6 and their LCM is 36. What is the difference between the largest and the smallest number?
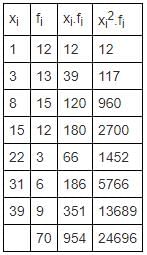
Following table represents the ages of some people.
Calculate the variance.
What is the value of (1/9) of [√169 X 3 + {62 + (3 ÷ 6 X 12)}] X (1/8) of [40 + {20 + (4 ÷ 16 X 16)}]?
What is the equation of line passing through midpoint of Points A(4, 3) and B(0, 7) having slope 3?
If 'a' and 'b' are roots of quadratic equation x2 + 4x - 21 = 0 such that b>a, then find the new quadratic equations whose roots will be (2a + 3b) and (2b - 3a).
A Metro train of 120 m length is running on a bridge at the rate of 40 km/hr. The train crosses the bridge in 20 second. What is the length of the bridge?
What is the value of 'a' in the following equation?
1/a of [{6.5 X (√100 − √4)} ÷ 13 X {2.5 X (√625 + √9)} ÷ 7] + 1/3 of √(15 ÷ 3 X 8 ÷ 4 - 1) = 6
If the sum of squares of length(l) and breadth(b) of a rectangle is 89 cm2 and its area is 40 cm2, then what is the area of a square having side equal to the breadth of rectangle(l>b)?
If a + 1/2a2 = 5, what is the value of (a - 5)49 + 1/249a98?