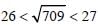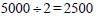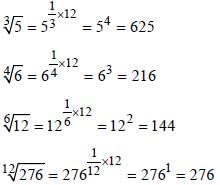SSC CGL Previous Year Questions: Number System and HCF & LCM- 1 - SSC CGL MCQ
20 Questions MCQ Test SSC CGL Previous Year Papers - SSC CGL Previous Year Questions: Number System and HCF & LCM- 1
If A is the smallest three digit number divisible by both 6 and 7 and B is the largest four digit number divisible by both 6 and 7, then what is the value of B – A? (SSC MTS 2018)
What is the median of the given data?
41, 43, 46, 50, 85, 61, 76, 55, 68, 95 (SSC MTS 2018)
41, 43, 46, 50, 85, 61, 76, 55, 68, 95 (SSC MTS 2018)
What is the value of x so that the seven digit number 8439 x 53 is divisible by 99? (SSC CGL-2018)
If the six digit number 15x1y2 is divisible by 44, then (x + y) is equal to: (SSC CGL-2018)
Which among the following numbers is exactly divisible by 11,13 and 7? (SSC CHSL-2018)
If x = 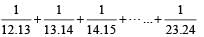
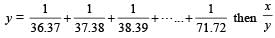 is equal to : (SSC CHSL-2018)
is equal to : (SSC CHSL-2018)
The square root of which of the following is a rational number? (SSC Sub. Ins. 2018)
Two numbers are in the ratio 4 : 7. If their HCF is 26, then the sum of these two numbers will be: (SSC Sub. Ins. 2018)
If the seven digit number 74x29y6 is divisible by 72, then what will be the value of (2x + 3y)? (SSC Sub. Ins. 2018)
What is the sum of the digits of the least number, which when divided by 12,16 and 54, leaves the same remainder 7 in each case, and is also completely divisible by 13? (SSC Sub. Ins. 2018 )
If 34N is divisible by 11, then what is the value of N? (SSC Sub. Ins. 2017)
Which one among 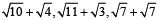 is the smallest number? (SSC Sub. Ins. 2017)
is the smallest number? (SSC Sub. Ins. 2017)
What is the smallest value that must be added to 709, so that the resultant is a perfect square? (SSC Sub. Ins. 2017)
Of the three numbers, the first is twice the second, and the second is twice the third. The average of the reciprocal of the numbers is 7/12. The numbers are: (SSC MTS 2017)
The least number of five digits exactly divisible by 88 is: (SSC MTS 2017)
Product of digits of a 2–digit number is 27. If we add 54 to the number, the new number obtained is a number formed by interchange of the digits. Find the number. (SSC CHSL 2017)
What is the LCM (least common multiple) of 57 and 93? (SSC CHSL 2017)
By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)
Which value among 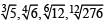 is the largest? (SSC CGL 2017)
is the largest? (SSC CGL 2017)
How many numbers are there from 300 to 650 which are completely divisible by both 5 and 7? (SSC CGL 2017)
|
319 docs|337 tests
|




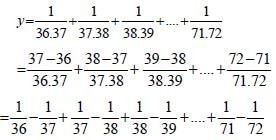
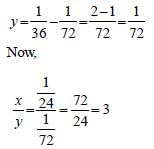
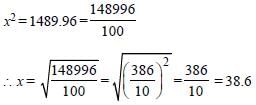
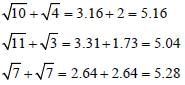
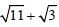 is the smallest number.
is the smallest number.