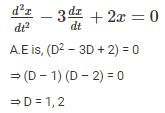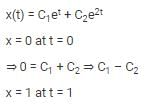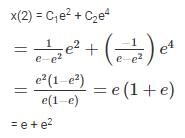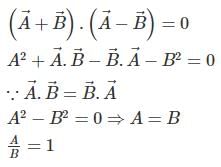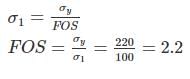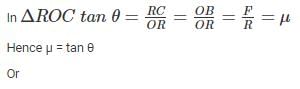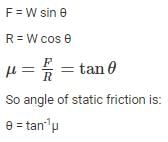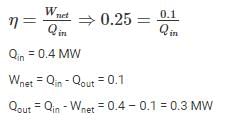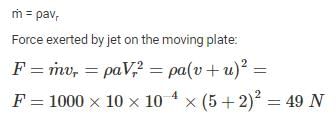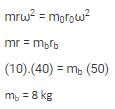Sample GATE Mock Test Mechanical Engineering (ME) - Mechanical Engineering MCQ
30 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Sample GATE Mock Test Mechanical Engineering (ME)
Identify the correct spelling of the word.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
She is brave. Her brother is more brave.
Select the most suitable sentence with respect to grammar and usage.
When a four digit number is divided by 65, it leaves a remainder of 29. If the same number is divided by 13, the remainder would be______
Complete the following sentence.
I was ___ ___ for the bus and then I ___ sight of Craig passing by.
4 – digit number greater than 5000 are randomly formed from the digits 0, 2, 3, 5 and 7. The probability of forming a number divisible by 5 when the digits are repeated is ______
It is theoretically possible that bacteria developed on Venus early in its history and that some were carried to Earth by a meteorite. However, strains of bacteria from different planets would probably have substantial differences in protein structure that would persist over time, and no two bacterial strains on Earth are different enough to have arisen on different planets. So, even if bacteria did arrive on Earth from Venus, they must have died out.
The argument is most vulnerable to which of the following criticisms?
A man sells three articles A, B, C and gains 10% on A, 20% on B and loses 10% on C. He breaks even when combined selling prices of A and C are considered, whereas he gains 5% when combined selling prices of B and C are considered. What is his net loss or gain on the sale of all the articles?
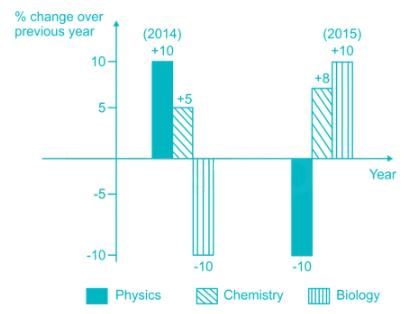
Which of the following inferences can be drawn from the above graph?
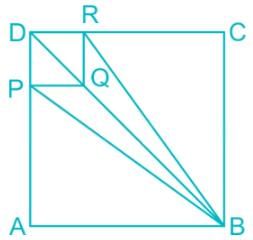
DRQP is a small square of side 'a' in the corner of a big square ABCD of side 'A'. What is the ratio of the area of the quadrilateral PBRQ to that of the square ABCD, given A/a = 3?
Let f(z) = (x2 + y2) + i2xy and g(z) = 2xy + i(y2 – x2) for z = x + iy ϵ C. Then, in the complex plane C.
If the Laplace transform of y(t) is given by 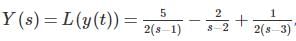 then y(0) + y'(0) = _____.
then y(0) + y'(0) = _____.
Consider the following statements P and Q:
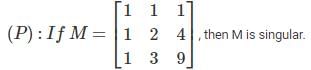
(Q): Let S be a diagonalizable matrix. If T is a matrix such that S + 5 T = I, then T is diagonalizable.
Which of the above statements hold TRUE?
Consider the differential equation
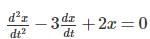 .If x = 0 at t = 0 and x = 1 at t = 1, the value of x at t = 2 is
.If x = 0 at t = 0 and x = 1 at t = 1, the value of x at t = 2 is
If for two vectors and , sum 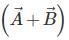 is perpendicular to the difference
is perpendicular to the difference  The ratio of their magnitude is
The ratio of their magnitude is
For an activity of duration 8 days in a network,
Total float = 10 days
Free float = 4 days
Independent float = 0
Then find no. of days an activity can be delayed without effecting project completion time is
Principal stress at a point in an elastic material are 100 MPa tensile, 50 MPa tensile and 25 MPa compressive. Determine the factor of safety against maximum principal stress theory. The elastic limit in simple tension is 220 MPa and Poisson’s Ratio is 0.3
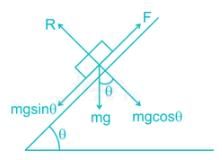
Which of the given formula is CORRECT for calculating the angle of static friction θs?
A steel shaft of 40 mm diameter is subjected to a twisting moment of 1200 N.m. What will be the maximum shear stress (in N/mm2)?
An engine operating at 25% efficiency produces work at a rate of 0.1 MW. At what rate (in MW) is heat exhausted into the surroundings?
In a 5 × 5 transportation problem, degeneracy would arise if the number of filled slots are
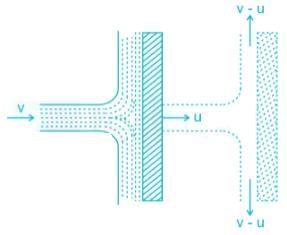
A horizontal water jet of area 10 cm2 and velocity 5 m/s strikes on a vertical plate which is moving with velocity 2 m/s towards the nozzle.
The force acting on the plane is _____ (in N)
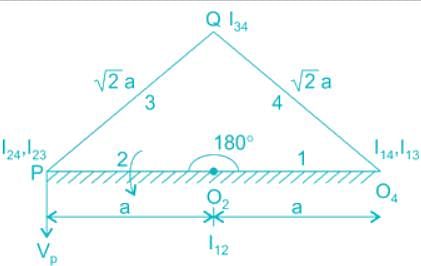
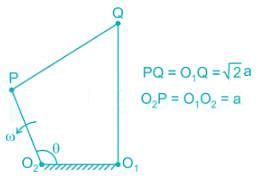
The input link O2P a four-bar linkage is rotated at ω rad/s. The angular velocity of the coupler PQ is 1 rad/s. Find the value of ω at an instant when θ is 180°.
A 250 mm thick slab of a nickel alloy is subjected to cold rolling using a roll of diameter 450 mm. If the angle of bite during rolling is 10°, the maximum reduction (in mm) during rolling is ___ (answer upto two decimal places)
An ideal gas is kept in thermal contact with a heat reservoir at 57°C while it is compressed from a volume of 20 L to a volume of 10 L. During the compression, an average force of 33.3 kN is used to move the piston a distance of 0.15 m. How much heat (in kJ) is exchanged between the gas and the reservoir?
Which of the following model does not fall in time series models?
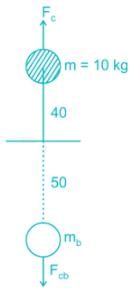
A wheel has an unbalance mass of 10 kg at a radius of 40 mm. Determine the balancing mass (in kg) required in the same plane opposite at a radial distance of 50 mm.
A 20 cm diameter spherical ball at 800 K is suspended in the air. Assuming that the ball closely approximates a black body. What will be the total amount of radiation emitted by the ball in 5 min in kJ. (σ = 5.67 × 10-8 W/m2K4)
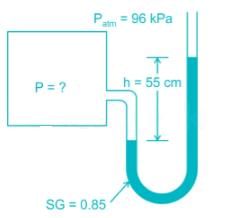
A manometer is used to measure the pressure of a gas in a tank. The fluid used has a specific gravity of 0.85 and the manometer column height is 55 cm, as shown in figure. If the local atmospheric pressure is 96 kPa, what is the absolute pressure in the tank?
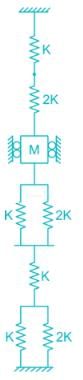
Find the natural frequency of the system.
|
29 docs|220 tests
|
|
29 docs|220 tests
|


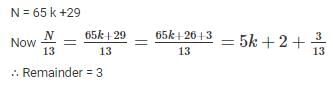
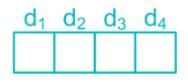
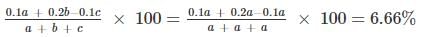
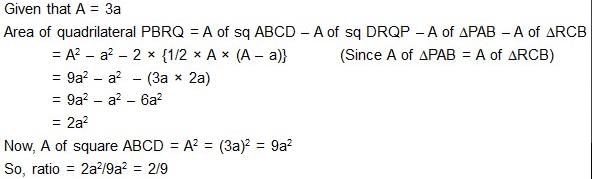
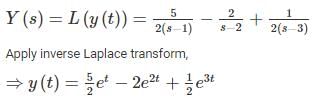
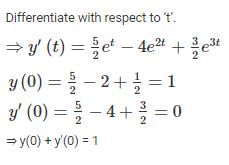
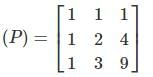
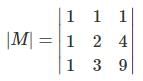

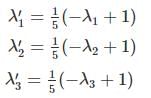
 will be distinct.
will be distinct.