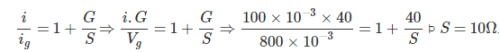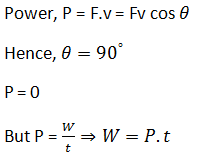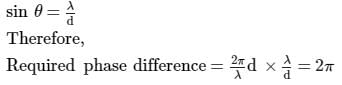Sample JEE Main Full Mock Test - JEE MCQ
30 Questions MCQ Test - Sample JEE Main Full Mock Test
The transition from the state n = 3 to n=1 in a hydrogen-like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from.
Eight drops of mercury of equal radii possessing equal charges combine to form a big drop. Then the capacitance of bigger drop compared to each individual small drop is
If the body is moving in a circle of radius r with a constant speed υ, its angular velocity is
To convert a 800 mV range milli voltmeter of resistance 40 Ω into a galvanometer of 100 mA range, the resistance to be connected as shunt is
A point charge q is placed at the centre of a skeleton cube made of thin non-conducting wire. The electric flux passing through one face of the cube is
The magnetic moment of a circular coil carrying current is
Consider the statement p: 'New Delhi is a city'. Which of the following is not negation of p?
The diameter of a cylinder is measured using a Vernier callipers with no zero error. It is found that the zero of the Vernier scale lies between 5.10 cm and 5.15 cm of the main scale. The Vernier scale has 50 divisions equivalent to 2.45 cm. The 24th division of the Vernier scale exactly coincides with one of the main scale divisions. The diameter of the cylinder is
The natural frequency of a L-C circuit is equal to
A coil of inductance 40 henry is connected in series with a resistance of 8 ohm and the combination is joined to the terminals of a 2 volt battery. The time constant of the circuit is
Proton and α-particles have the same de-Broglie wavelength. What is the same for both of them ?
The energy released in a typical nuclear fusion reaction is approximately
The angular velocity of the second needle in watch (in rad/s) is
After an interval of one day, 1/16th of the initial amount of a radioactive material remains in a sample. It's half life will be
Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
A straight wire of length l and electric dipole moment p is bent to form a semicircle. The new dipole moment would be
A block of mass 10 kg is placed on rough horizontal surface whose coefficient of friction is 0.5. If a horizontal force of 100 N is applied on it, then acceleration of block will be
A bird weighs 2 kg and is inside a closed cage of 1 kg. If it starts flying, then what is the weight of the bird and cage assembly
A particle of mass M and charge Q moving with velocity V → describes a circular path of radius R when subjected to a uniform transverse magnetic field of induction B. The work done by the field when the particle completes one full circle is
Which of the following is more effective in inducing nuclear fission
If a liquid does not wet the glass, then its angle of contact is
The kinetic energy k of a particle moving along a circle of radius R depends on the distance covered s as K = as2 where a is a constant. The force acting on the particle is
A 1 kg stationary bomb exploded in three parts having mass ratio 1:1:3 . Parts having same mass are moving in perpendicular direction with velocity 30m/s, then the velocity of bigger part will be
Two identical masses of 5 kg each fall on a wheel from a height of 10 m . The wheel disturbs a mass of 22 kg water, the rise in temperature of water will be :-
A parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction pattern is formed on a screen placed perpendicular to the direction of the incident beam. At the first minimum of the diffraction pattern, the phase difference between the rays coming from the two edges of slit is
Both light and sound waves produce diffraction. It is more difficult to observe the diffraction with light waves because
In Huygens wave theory, the locus of all points osculating in the same phase is called a



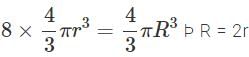 As capacity is r, hence capacity becomes 2 times.
As capacity is r, hence capacity becomes 2 times.