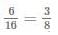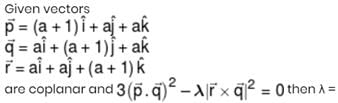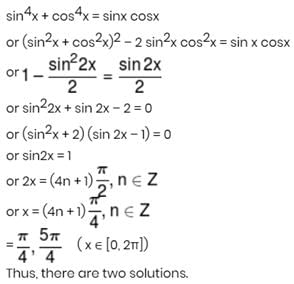Sample JEE Main Mathematics Mock Test - JEE MCQ
25 Questions MCQ Test - Sample JEE Main Mathematics Mock Test
y-axis divides the segment joining points (-3,-4) and (1,-2) in the ratio
A pair of tangent lines are drawn from the origin to the circle x2+y2+20(x+y)+20 = 0. The equation of pair of tangents is
If the polar w.r.t.y2 = 4ax touches the ellipse (x2/a2) + (y2/b2) = 1, the locus of its pole is
If f(x) = sinx-(x/2) is increasing function, then
The equation of the curve passing through the origin and satisfying the differential equation dy/dx = (x − y)2 is
In the following question, a
Statement-1 is given followed by a corresponding
Statement-2 just below it. Read the statements carefully and mark the correct answer-
Consider the system of equations
ax+by = 0, cx+dy = 0, where a, b, c, d ∈ {0,1}
Statement-1: The probability that the system of equations has a unique solution is 3/8 .
Statement-2: The probability that the system of equations has a solution is 1.
The maximum area of the rectangle that can be inscribed in a circle of radius r is
If z ≠ 0 is a complex number such that Arg (z) = π/4, then
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion (A): Angle between the vectors
Reason (R): If θ is the angle between
The number of distinct permutations of the letters of the word STATISTICS that begin and end with the letter S is
If A and B are two events and B is a subset of A, then P(A/B) is equal to
If A and B are such events that P(A)>0 and P(B)≠1, then P(A̅/B̅) is equal to
If x2 + px + q is the quadratic equation whose roots are a - 2 and b - 2 where a and b are the roots of x2 - 3x + 1 = 0, then
The A.M., H.M. and G.M. between two numbers are 144/15, 15 and 12, but not necessarily in this order. Then H.M., G.M. and A.M. respectively are
If lines y = 3x+1 and 2y = x+3, are equally inclined with y = mx+4, m =
If the difference between mean and mode is 63 then the difference between mean and median is:-
How many ways 5 balls can be placed in 3 boxes such that no box remains empty if balls as well as boxes are identical ?
The total number of solution of sin4x + cos4x = sinx cosx in [0, 2π] is equal to :-
By using 2, 4, 5, 7, 8, 9 how many three digit numbers are formed in form xyz when x + y + z is even. (repitition not allowed).



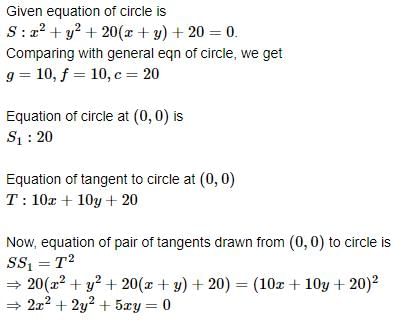

 where a, b, c, d {0, 1}
where a, b, c, d {0, 1}