Test: CAT Quantitative Aptitude- 8 - CAT MCQ
22 Questions MCQ Test - Test: CAT Quantitative Aptitude- 8
A cylindrical well of depth 15 m and radius 6 m is dug at a place to fetch water from it. The well is lined from inside with a layer of bricks of thickness 1 m. In rainy season the well is filled to the brim. Find the volume of water in the well at that time.
Tap A can fill a tank in 16 hours. Another tap B is opened 2 hours after opening of tap A and it takes 4 more hours to fill the tank. How many minutes will tap B alone require to fill the entire tank?
The number 35a246772 is in base 9. This number when written in base 10 is divisible by 8. Find the value of digit a.
Harry forgot his 7 digit driving licence number which he wanted to write. However, he remembered that the digit 1 appeared exactly once in the number and the remaining 6 digits were 3 non-zero digits, each appearing exactly twice. What is the minimum number of different numbers that Harry would have to write, to be certain of writing the right number?
Which of the following is true about the absolute difference between a two- digit number and the number obtained by reversing its digits?
If team India has played (4/5)th of total 40 matches and wins 29 matches, then the maximum number of matches it can afford to lose from the remaining matches to maintain a more than 75% win record?
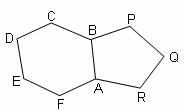
In the figure, ABCDEF is a regular hexagon and ABPQR is a regular pentagon. The side AB is common. Calculate ∠AFR (in degrees).
An alloy of gold and silver weighs 50 gm. It contains 80% gold. How many grams of gold should be added to the alloy so that percentage of gold increases to 90?
How many acute-angled triangles can be formed with sides 5 cm, 12 cm and x cm, if x is an integer.
In a 100 km car race, Car-1 can beat Car-2 by 10 km and Car-3 by 20 km. In a certain 500 km race, if Car-1 starts from a point 50 km behind the starting point, Car-2 starts from the starting point and Car-3 starts 50 km ahead of the starting point, then which of the following cars shall win the race?
(Enter your answer as 1 for Car-1, 2 for Car-2, and so on.)
A certain number of chocolates are equally distributed among a certain number of students in such a way that each student gets 14 chocolates. However, if 4 of those students decide to distribute their chocolates equally amongst themselves, then the students who have not distributed their share get 4 extra chocolates. Find the total number of chocolates.
Mitali has 2 watches one is Polex and the other is Tastfrack. At 7:00 am on Friday, 1st January 2016 (which is the correct time) Polex shows 6:22 am while Tastfrack shows 7:57 am. Polex gains 2 minutes and Tastfrack loses 3 minutes every hour. At what time and date will both watches show same time for first instance?
What is the number of sides of the regular polygon whose interior angle is four times of the exterior angle?
If A is the set of all natural numbers divisible by 3 upto 100, B is the set of all even natural numbers upto 100, C is the set of all natural numbers divisible by 7 upto 100 and D is the set of all the perfect squares from 1 to 100, then find the sum of all the numbers in (A ∩ C) ∪ (B ∩ D).
A number 242a27b is divisible by 18, what is the value of (a, b)?
Meena invested Rs. 5,000 in a scheme offering 8% interest p.a. compounded annually for two years while Seema invested some amount in another scheme offering 12% simple interest for two years. If the interest received by Seema after 2 years was 30.77% more than that received by Meena, then find the approximate amount invested by Seema in the scheme.
How many solutions does the inequalty x2 < - 16 hold, if x is a real number?
Find the selling price (in Rs.) of a sari after successive discounts of 20%, 25% and 30% on the marked price of Rs. 700.
Area of an equilateral triangle is 8√3 cm2 . A circle passes through the incentre of the triangle such that one side of the triangle is chord to the circle such that the other two sides of the triangle are tangent to the circle. Find the area of the circle.
A chocolate selling firm manufactures one chocolate for Rs. 20 and sells them in a box of chocolates at Rs. 960 per box such that each box contains 40 chocolates. If the firm now increases the quantity of chocolates per box by 15%, find the increase (in Rs.) in the selling price per box, so that the percent profit increases by 5 percent points.
A train 440 metres long passes a railway platform 876 metres long in 10 seconds. How many seconds will it take to pass a running train 990 metres long?
If the angle formed by the diagonal (passing through the centre of the polygon) with one of the sides of a regular polygon is 7π/ 16, find the number of distinct lines which can be drawn between all the vertices of that polygon.



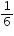 = 120°
= 120°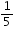 = 108°
= 108°