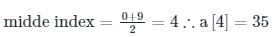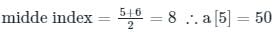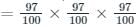Searching Algorithms - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Searching Algorithms
For which of the following tasks, stack is not suitable data structure?
(a) Binary search in an array
(b) Breadth first search
(c) Implementing function calls
(d) Process scheduling
(a) Binary search in an array
(b) Breadth first search
(c) Implementing function calls
(d) Process scheduling
Which open addressing technique is free from Clustering problems?
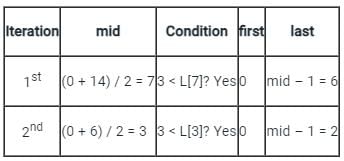
Consider the array L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. Suppose you’re searching for the value 3 using binary search method. What is the value of the variable last after two iterations?
Example 1:
Consider array has 4 elements and a searching element 16.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T1
Example 2:
Consider array has 4 elements and a searching element 22.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T2
Note: Searching is successful.
Q.Which of the following statement are true?
Example 1:
Consider array has 4 elements and a searching element 16.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T1
Example 2:
Consider array has 4 elements and a searching element 22.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T2
Note: Searching is successful.
Which of the following statement are true?
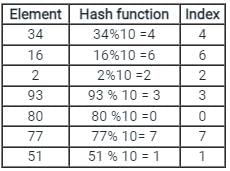
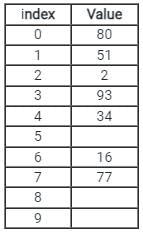
When two elements map to the same slot in the hash table, it is called ____________?
Consider a hash table of size 7, with hash function H (k) = k % 7, and pseudo random i = (i + 5) % 7. We want to insert the following keys one by one from left to right.
15, 11, 25, 16, 9, 8, 12
What will be the position of the key 25, if we use random probing?
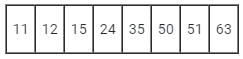
What is the worst-case and average-case time complexity of the Binary search?
Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions?
|
55 docs|215 tests
|
|
55 docs|215 tests
|