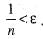Sequences And Series Of Real Numbers -3 - IIT JAM MCQ
20 Questions MCQ Test - Sequences And Series Of Real Numbers -3
If Sn denoted the sum of n term of the series 

If ai > 0 for i = 1, 2, 3,..,n and a1, a2, a3, ...an = 1 then the greatest value of (1 + a1)(1 + a2)... (1 + an) is:
Let < Sn > and <tn> be two sequences such that 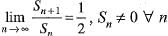 and
and 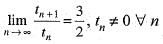 Then,
Then,
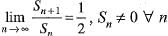 and
and 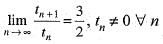 Then,
Then,For infinite series 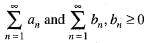 for n, and there is a real number N, such that for n ≥ N implies |an|≤ bn. If
for n, and there is a real number N, such that for n ≥ N implies |an|≤ bn. If 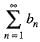 coverges, then
coverges, then
If a sequence  converges to a real number A, then
converges to a real number A, then 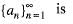
If a sequence is not a Cauchy sequence, then it is a
 is an increasing bounded sequence, then for the sequence
is an increasing bounded sequence, then for the sequence 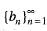 is following statement is false
is following statement is false
If a sequence < an2 > converges to a2, then the sequence < an > converges to
A real number l is a limit point of a sequence < an> if and only if there exists
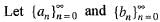 be tw0 sequence such that
be tw0 sequence such that  converges respectively to A and AB, then
converges respectively to A and AB, then 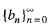 converges Iff
converges Iff
Let sequence 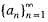 converges to A and sequence
converges to A and sequence 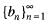 converges to B, with an ≤ bn for all n, then
converges to B, with an ≤ bn for all n, then
A : Cauchy sequence is convergent.
B : Cauchy sequence is bounded in R.
Let San be a convergent series of positive terms and let Sbn be a divergent series of positive terms. Then,
Which of the following statement is true?
Let {an} be a sequence of real numbers. Then 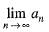 exists if and only if
exists if and only if
Let < an> ≥ a. Let for every positive integer k, Ak be the set of all positive integer n such that | an- a | ≤ 1/k. Then,


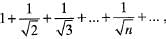 then Sn will be >
then Sn will be > 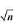 Explanation:
Explanation:
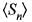 be a sequence such that
be a sequence such that  and
and 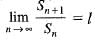
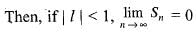
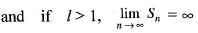

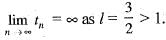
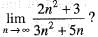
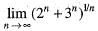 is equal to
is equal to