Test: Sorting- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Sorting- 2
The number of elements that can be sorted in 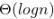 time using heap sort is
time using heap sort is
Given an array where numbers are in range from 1 to n6, which sorting algorithm can be used to sort these number in linear time?
In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?
Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then
Let P be a QuickSort Program to sort numbers in ascending order using the first element as pivot. Let t1 and t2 be the number of comparisons made by P for the inputs {1, 2, 3, 4, 5} and {4, 1, 5, 3, 2} respectively. Which one of the following holds?
You have an array of n elements. Suppose you implement quicksort by always choosing the central element of the array as the pivot. Then the tightest upper bound for the worst case performance is
In a permutation a1.....an of n distinct integers, an inversion is a pair (ai, aj) such that i < j and ai > aj. What would be the worst case time complexity of the Insertion Sort algorithm, if the inputs are restricted to permutations of 1.....n with at most n inversions?
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
Which of the following changes to typical QuickSort improves its performance on average and are generally done in practice.
1) Randomly picking up to make worst case less likely to occur.
2) Calling insertion sort for small sized arrays to reduce recursive calls.
3) QuickSort is tail recursive, so tail call optimizations can be done.
4) A linear time median searching algorithm is used to pick the median, so that the worst case time reduces to O(nLogn)
Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n(≥ 2) numbers? In the recurrence equations given in the options below, c is a constant.
Assume that a mergesort algorithm in the worst case takes 30 seconds for an input of size 64. Which of the following most closely approximates the maximum input size of a problem that can be solved in 6 minutes?
The worst case running times of Insertion sort, Merge sort and Quick sort, respectively, are:
Assume that the algorithms considered here sort the input sequences in ascending order. If the input is already in ascending order, which of the following are TRUE?
I. Quicksort runs in Θ(n2) time
II. Bubblesort runs in Θ(n2) time
III. Mergesort runs in Θ(n) time
IV. Insertion sort runs in Θ(n) time
Assume that we use Bubble Sort to sort n distinct elements in ascending order. When does the best case of Bubble Sort occur?
If we use Radix Sort to sort n integers in the range (nk/2,nk], for some k>0 which is independent of n, the time taken would be?
Consider an array of elements arr[5]= {5,4,3,2,1} , what are the steps of insertions done while doing insertion sort in the array.
Which is the correct order of the following algorithms with respect to their time Complexity in the best case?
Which of the following statements is correct with respect to insertion sort?
*Online - can sort a list at runtime
*Stable - doesn't change the relative order of elements with equal keys.
Consider the array A[]= {5,4,9,1,3} apply the insertion sort to sort the array. Consider the cost associated with each sort is 25 rupees , what is the total cost of the insertion sort when element 1 reaches the first position of the array?


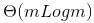 for m input elements. For m =
for m input elements. For m = 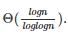 , the value of
, the value of  will be
will be 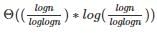 which is
which is 

















