Test (No calculator) - 1 - SAT MCQ
10 Questions MCQ Test - Test (No calculator) - 1
On Saturday afternoon, Armand sent m text messages each hour for 5 hours, and Tyrone sent p text messages each hour for 4 hours. Which of the following represents the total number of messages sent by Armand and Tyrone on Saturday afternoon?
Kathy is a repair technician for a phone company. Each week, she receives a batch of phones that need repairs. The number of phones that she has left to fix at the end of each day can be estimated with the equation P = 108 − 23d, where P is the number of phones left and d is the number of days she has worked that week. What is the meaning of the value 108 in this equation?
(x2y −3y2 + 5xy2) − (−x2y + 3xy2 − 3y2)
Which of the following is equivalent to the expression above?
h = 3a + 28.6
A pediatrician uses the model above to estimate the height h of a boy, in inches, in terms of the boy’s age a, in years, between the ages of 2 and 5. Based on the model, what is the estimated increase, in inches, of a boy’s height each year?

The formula above gives the monthly payment m needed to pay off a loan of P dollars at r percent annual interest over N months. Which of the following gives P in terms of m, r, and N?
3x + 4y = −23
2y − x = −19
What is the solution (x, y) to the system of equations above?
g (x) = ax2 + 24
For the function g defined above, a is a constant and g (4) = 8. What is the value of g (− 4)?


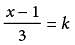 and k =3, what is the value of x?
and k =3, what is the value of x?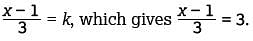 Multiplying both sides of
Multiplying both sides of 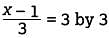 gives x -1 = 9 and then adding 1 to both sides of x- 1 = 9 gives x = 10.
gives x -1 = 9 and then adding 1 to both sides of x- 1 = 9 gives x = 10.
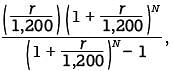 multiplying both
multiplying both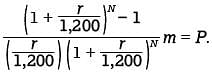
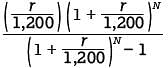 rather than by the reciprocal of this expression
rather than by the reciprocal of this expression  Choices C and D are incorrect and are likely the result of errors while trying to solve for P.
Choices C and D are incorrect and are likely the result of errors while trying to solve for P.