Test (With calculator) - 2 - SAT MCQ
10 Questions MCQ Test - Test (With calculator) - 2
Which of the following numbers is NOT a solution of the inequality 3x − 5 ≥ 4x − 3?

Based on the histogram above, of the following, which is closest to the average (arithmetic mean) number of seeds per apple?

Based on the histogram above, of the following, which is closest to the average (arithmetic mean) number of seeds per apple?
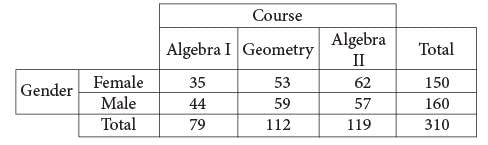
A group of tenth-grade students responded to a survey that asked which math course they were currently enrolled in.
The survey data were broken down as shown in the table above. Which of the following categories accounts for approximately 19 percent of all the survey respondents?

A group of tenth-grade students responded to a survey that asked which math course they were currently enrolled in.
The survey data were broken down as shown in the table above. Which of the following categories accounts for approximately 19 percent of all the survey respondents?
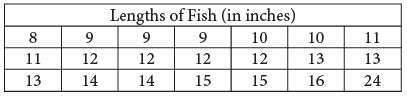
The table above lists the lengths, to the nearest inch, of a random sample of 21 brown bullhead fish. The outlier measurement of 24 inches is an error. Of the mean, median, and range of the values listed, which will change the most if the 24-inch measurement is removed from the data?
What does the C-intercept represent in the graph?
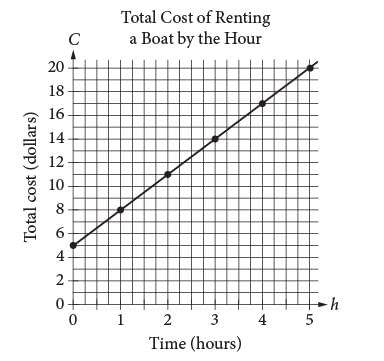
The graph above displays the total cost C, in dollars, of renting a boat for h hours.
Question refer to the following information.

Which of the following represents the relationship between h and C?
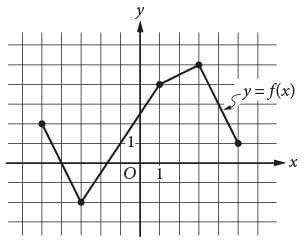
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f (x) at its minimum?
y < -x + a
y > x + b
In the xy-plane, if (0, 0) is a solution to the system of inequalities above, which of the following relationships between a and b must be true?
A food truck sells salads for $6.50 each and drinks for $2.00 each. The food truck’s revenue from selling a total of 209 salads and drinks in one day was $836.50. How many salads were sold that day?
Alma bought a laptop computer at a store that gave a 20 percent discount off its original price. The total amount she paid to the cashier was p dollars, including an 8 percent sales tax on the discounted price. Which of the following represents the original price of the computer in terms of p?



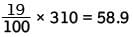 respondents. Of the choices given, 59, the number of males taking Geometry, is closest to 58.9 respondents.
respondents. Of the choices given, 59, the number of males taking Geometry, is closest to 58.9 respondents.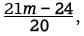 which is a change of inches. Since m must be between the smallest and largest measurements of the 21 fish, it follows that 8 < m < 24, from which it can be seen that the change in the mean, in inches, is
which is a change of inches. Since m must be between the smallest and largest measurements of the 21 fish, it follows that 8 < m < 24, from which it can be seen that the change in the mean, in inches, is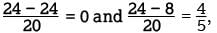 and so must be less than the change in the range, 8 inches. Choice B is incorrect because the median length of the 21 fish represented in the table is 12, and after the 24-inch measurement is removed, the median of the remaining 20 lengths is also 12. Therefore, the change in the median (0) is less than the change in the range (8). Choice D is incorrect because the changes in the mean, median, and range of the measurements are different.
and so must be less than the change in the range, 8 inches. Choice B is incorrect because the median length of the 21 fish represented in the table is 12, and after the 24-inch measurement is removed, the median of the remaining 20 lengths is also 12. Therefore, the change in the median (0) is less than the change in the range (8). Choice D is incorrect because the changes in the mean, median, and range of the measurements are different.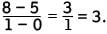 Therefore,
Therefore,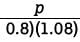 in terms of p.
in terms of p.















