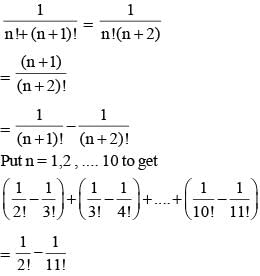Test: Algebra - 1 - CAT MCQ
30 Questions MCQ Test - Test: Algebra - 1
If a1 + a2 + a3 + ... + an = 3(2n+1 – 2), for every n ≥ 1, then a11 equals
(2019)
The number of solutions to the equation |x|(6x2 + 1) = 5x2 is
(2019)
The product of the distinct roots of |x2 – x – 6| = x + 2 is
(2019)
The number of the real roots of the equation 2cos (x(x + 1)) = 2x + 2–x is
(2019)
For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd. If m is a positive integer such that 8f(m + 1) – f(m) = 2, then m equals
(2019)
Consider a function f satisfying f (x + y) = f (x) f (y) where x, y are positive integers, and f (1) = 2. If f (a + 1) + f (a + 2) + ... + f (a + n) = 16(2n – 1) then a is equal to
(2019)
What is the largest positive integer n such that 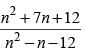 is also a positive integer?
is also a positive integer?
(2019)
If 5x – 3y = 13438 and 5x – 1 + 3y + 1 = 9686, then x + y equals
(2019)
The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 + c?
(2019)
Let a, b, x, y be real numbers such that a2 + b2 = 25, x2 + y2 = 169, and ax + by = 65. If k = ay – bx, then
(2019)
If u2 + (u − 2v − 1)2 = −4v(u + v), then what is the value of u + 3v?
(2018)
If f(x) = 5x + 2 / 3x - 5 and g(x) = x2 – 2x – 1, then the value of g (f(f(3))) is
(2017)
The number of solutions (x, y, z) to the equation x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12,and z ≤ 12 is
(2017)
Suppose, log3 x = log12 y = a, where x, y are positive numbers. If G is the geometric mean of x and y, and log6 G is equal to
(2017)
If the sum to infinity of the series 2 + (2 – d) 2/3 + (2 + d) 4/9 + (2 + 3d) 8/27 + .... is 5/2, what is the value of d?
(2016)
If S = 2/10 + 6/102 + 12/103 + 20/104 + 30/105 + 42/106 + ......., find the value of S?
(2016)
If the roots of the equation (x + 1) (x + 9) + 8 = 0 are a and b, then the roots of the equation (x + a) (x + b) – 8 = 0 are
(2016)
If x2 + (x + 1) (x + 2) (x + 3) (x + 6) = 0, where x is a real number, then one value of x that satisfies this equation is
(2015)
Find the solution set for [x] + [2x] + [3x] = 8, where x is a real number and [x] is the greatest integer less than or equal to x.
(2015)
If 3x + y + 4 = 2xy, where x and y are natural numbers, then find the ratio of the sum of all possible values of x to the sum of all possible values of y.
(2015)
Let x, y, z and t be the positive numbers which satisfy the following conditions:
I. If x > y, then z > t and
II. If x > z, then y < t
Which of the following is necessarily true?
(2015)
Both the roots of the quadratic equation x2 + rx + s = 0 are real and greater than 1. If 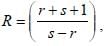 then which of the following is definitely true?
then which of the following is definitely true?
(2015)
What is the sum of the roots of all the quadratic equations that can be formed such that both the roots of the quadratic equation are common with the roots of equation (x – a) (x – b) (x – c) = 0?
(2014)
The sum of the coefficients of the polynomial (x – 1)9 (x – 2)4 (x – 4) is
(2014)
An equation with all positive roots is written as Xn + anXn-1 + an-1Xn-2 + .... a1 = 0. Which of the following in necessarily true?
(2014)
The coefficient of a12b8 in the expansion of (a2 + b)13 is
(2013)
Let R(x) = mx3 – 100x2 + 3n, where m and n are positive integers. For how many ordered pairs (m, n) will (x – 2) be a factor of R(x)?
(2013)


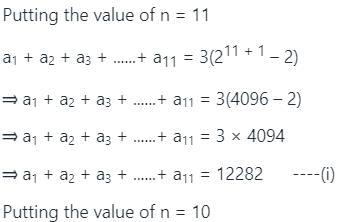

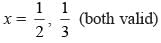
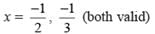

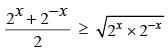

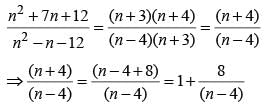
 is non-negative integer.
is non-negative integer.
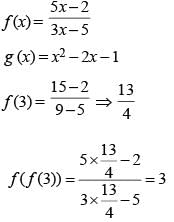

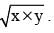
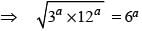
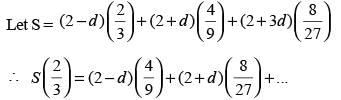
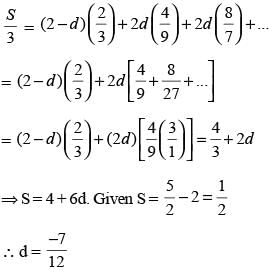
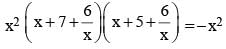
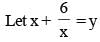
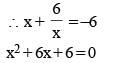
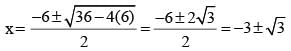
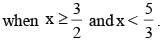
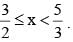
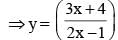

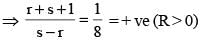
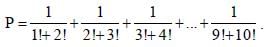 Find the value of P.
Find the value of P.