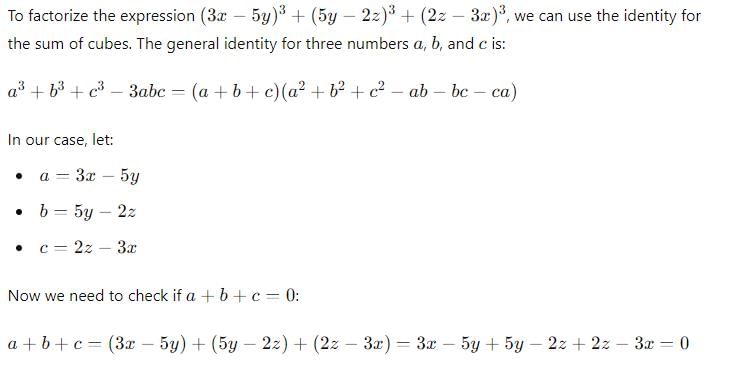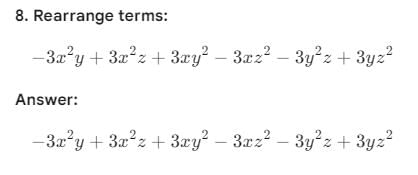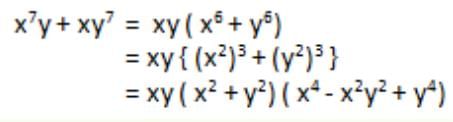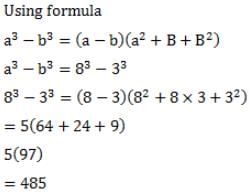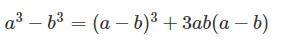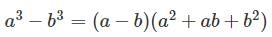Class 9 Exam > Class 9 Tests > Mathematics (Maths) Class 9 > Test: Algebraic Identities Cubic Type - Class 9 MCQ
Test: Algebraic Identities Cubic Type - Class 9 MCQ
Test Description
20 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Algebraic Identities Cubic Type
Test: Algebraic Identities Cubic Type for Class 9 2025 is part of Mathematics (Maths) Class 9 preparation. The Test: Algebraic Identities Cubic Type questions and answers have been
prepared according to the Class 9 exam syllabus.The Test: Algebraic Identities Cubic Type MCQs are made for Class 9 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Algebraic Identities Cubic Type below.
Solutions of Test: Algebraic Identities Cubic Type questions in English are available as part of our Mathematics (Maths) Class 9 for Class 9 & Test: Algebraic Identities Cubic Type solutions in
Hindi for Mathematics (Maths) Class 9 course. Download more important topics, notes, lectures and mock
test series for Class 9 Exam by signing up for free. Attempt Test: Algebraic Identities Cubic Type | 20 questions in 20 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study Mathematics (Maths) Class 9 for Class 9 Exam | Download free PDF with solutions
Test: Algebraic Identities Cubic Type - Question 1
Expansion and simplification of 8(3h - 4) + 5(h - 2) gives
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 1
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 2
Test: Algebraic Identities Cubic Type - Question 3
Factorise:(3x- 5y)3+ (5y – 2z)3 + (2z – 3x)3
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 3
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 4
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 5
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 6
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 7
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 8
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 9
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 10
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 11
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 12
Test: Algebraic Identities Cubic Type - Question 13
What is the value 83 – 33 (without solving the cubes)?
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 13
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 14
Test: Algebraic Identities Cubic Type - Question 15
What is the value of 53 – 13(without solving cube)?
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 15
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 16
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 17
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 18
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 19
Detailed Solution for Test: Algebraic Identities Cubic Type - Question 20
|
40 videos|420 docs|51 tests
|
Information about Test: Algebraic Identities Cubic Type Page
In this test you can find the Exam questions for Test: Algebraic Identities Cubic Type solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Algebraic Identities Cubic Type , EduRev gives you an ample number of Online tests for practice