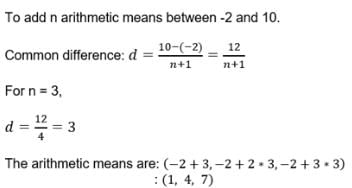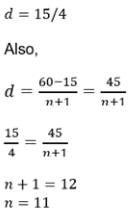Test: Arithmetic Mean - JEE MCQ
10 Questions MCQ Test - Test: Arithmetic Mean
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be
For what value of n,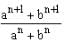 is the arithmetic mean (AM) of a and b?
is the arithmetic mean (AM) of a and b?
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.
A man saved Rs 21700 in 14 years. In each year after the first he saved Rs 100 more than he did in the preceding year. How much did he save in the first year?
What is the 10th A.M between 2 and 57 if 10 A.M s are inserted between these numbers?
If n numbers are inserted between 15 and 60 such that the ratio of the first to the last is 1 : 3, then the value of n is:
If A1, A2, A3,…., An are n numbers between a and b, such that a, A1, A2, A3,…, An, b are in A.P., then nth term from beginning is: