Test: Arun Sharma Based Level 2: Time & Work - CAT MCQ
15 Questions MCQ Test - Test: Arun Sharma Based Level 2: Time & Work
Directions for Question: Study the following and answer the questions that follow.
A gas cylinder can discharge gas at the rate of 1 cc/minute from burner A and at the rate of 2 cc/minute from burner B (maximum rates of discharge). The capacity of the gas cylinder is 1000 cc of gas.
The amount of heat generated is equal to 1 kcal per cc of gas.
However, there is a wastage of the heat as per follows :
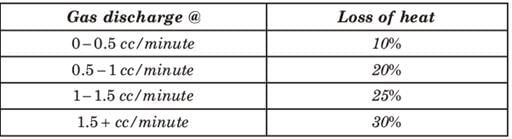
@ (Include higher extremes)
Q. If both burners are opened simultaneously such that the first is opened to 90% of its capacity and the second is opened to 80% of its capacity, the amount of time in which the gas cylinder will be empty (if it was half full at the start) will be:
The amount of heat generated is equal to 1 kcal per cc of gas.

@ (Include higher extremes)
Directions for Question: Study the following and answer the questions that follow.
A gas cylinder can discharge gas at the rate of 1 cc/minute from burner A and at the rate of 2 cc/minute from burner B (maximum rates of discharge). The capacity of the gas cylinder is 1000 cc of gas.
The amount of heat generated is equal to 1 kcal per cc of gas.
However, there is wastage of the heat as per follows:

@ (Include higher extremes)
Q. The maximum amount of heat with fastest speed of cooking that can be utilised for cooking will be when:
The amount of heat generated is equal to 1 kcal per cc of gas.

@ (Include higher extremes)
Directions for Question: Study the following and answer the questions that follow.
A gas cylinder can discharge gas at the rate of 1 cc/minute from burner A and at the rate of 2 cc/minute from burner B (maximum rates of discharge). The capacity of the gas cylinder is 1000 cc of gas.
The amount of heat generated is equal to 1 kcal per cc of gas.
However, there is wastage of the heat as per follows :

@ (Include higher extremes)
Q. The amount of heat utilised for cooking if a full gas cylinder is burnt by opening the aperture of burner A 100% and that of burner B 50% is
The amount of heat generated is equal to 1 kcal per cc of gas.

@ (Include higher extremes)
Directions for Question: Study the following and answer the questions that follow.
A gas cylinder can discharge gas at the rate of 1 cc/minute from burner A and at the rate of 2 cc/minute from burner B (maximum rates of discharge). The capacity of the gas cylinder is 1000 cc of gas.
The amount of heat generated is equal to 1 kcal per cc of gas.
However, there is wastage of the heat as per follows:

@ (Include higher extremes)
Q. For Question 3, if burner A had been opened only 25% and burner B had been opened 50%, the amount of heat available for cooking would be
Directions for Question: Study the following and answer the questions that follow.
A gas cylinder can discharge gas at the rate of 1 cc/minute from burner A and at the rate of 2 cc/minute from burner B (maximum rates of discharge). The capacity of the gas cylinder is 1000 cc of gas.
The amount of heat generated is equal to 1 kcal per cc of gas.
However, there is wastage of the heat as per follows :

@ (Include higher extremes)
Q. For Question 4, the amount of time required to finish a full gas cylinder will be
A group of workers can complete a certain job in 9 days. But it so happens that every alternate day starting form the second day, two workers are withdrawn from the job and every alternate day starting from the third day, one worker is added to the group. In such a way, the job is finished by the time, there is no worker left. If it takes the double time to finish the job now, find the number of workers who started the job?
A student studying the weather for d days observed that
(i) It rained on 7 days, morning or afternoon,
(ii) When it rained in the afternoon, it was clear in the morning,
(iii) There were five clear afternoons, and
(iv) There were six clear mornings. Then, d equals.
Sumit constructs a wall working in a special way and takes 12 days to complete it. If Sn is the length of the wall (in m) that he constructs on the nth day, then
Sn = 2n, 0 ≤ n ≤ 4
Sn = 8, for n = 5
Sn = 3n - 7, 6 ≤ n ≤ 12
Find the total length of the wall he constructs in the first 10 days.
Alok, Mithilesh, and Bimlesh started a work and after completing 1 / 5th of the work Bimlesh left. Alok and Mithilesh then worked for 20 days. Bimlesh then took over from Alok and Mithilesh and completed the remaining portion of the work in 12 days. If Bimlesh takes 40 days to complete the work, in how many days would Alok alone or Mithilesh alone complete the work if the efficiencies with which they work is the same?
Sixty-for men working 8 hrs a day plan to complete a piece of work in 9 days. However, 5 days later they found that they had completed only 40% of the work. They now wanted to finish the remaining portion of the work in 4 more days. How many hours per day should they need to work in order to achieve the target?
Direction for Question : Read the passage below and solve the questions based on it.
Hi-Choice Dressers received a large order for stitching uniforms from A.R. Academy and T.M. High School. He has two cutters who will cut the fabric, five tailors who will do the stitching, and two assistants to stitch the buttons and button holes. Each of these nine persons will work for exactly 10hrs a day. Each of the A.R. Academy uniform requires 20 min for cutting the fabric, 1hr for doing the stitching and 15 min for stitching the buttons and the button holes. The T.M. High School uniform requires 30 min, 1hrs and 30 min, respectively, for the same activities.
Q. On a particular day, Hi-Choice Dressers decided to complete 20 T.M. High School uniforms. How many A.R. Academy uniforms can it complete on that day?
Direction for Question : Read the passage below and solve the questions based on it.
Hi-Choice Dressers received a large order for stitching uniforms from A.R. Academy and T.M. High School. He has two cutters who will cut the fabric, five tailors who will do the stitching, and two assistants to stitch the buttons and button holes. Each of these nine persons will work for exactly 10hrs a day. Each of the A.R. Academy uniform requires 20 min for cutting the fabric, 1hr for doing the stitching and 15 min for stitching the buttons and the button holes. The T.M. High School uniform requires 30 min, 1hrs and 30 min, respectively, for the same activities.
Q. If Hi-Choice Dressers decided to complete 30 T.M. High School uniforms only and no other uniform on that particular day, how many total man-hours will go idle?
Direction for Question : Read the passage below and solve the questions based on it.
Hi-Choice Dressers received a large order for stitching uniforms from A.R. Academy and T.M. High School. He has two cutters who will cut the fabric, five tailors who will do the stitching, and two assistants to stitch the buttons and button holes. Each of these nine persons will work for exactly 10hrs a day. Each of the A.R. Academy uniform requires 20 min for cutting the fabric, 1hr for doing the stitching and 15 min for stitching the buttons and the button holes. The T.M. High School uniform requires 30 min, 1hrs and 30 min, respectively, for the same activities.
Q. If Hi-Choice Dressers hires one more assistant, what is the maximum number of A.R. Academy uniforms that can be completed in a day?
Direction for Question : Read the passage below and solve the questions based on it.
Hi-Choice Dressers received a large order for stitching uniforms from A.R. Academy and T.M. High School. He has two cutters who will cut the fabric, five tailors who will do the stitching, and two assistants to stitch the buttons and button holes. Each of these nine persons will work for exactly 10hrs a day. Each of the A.R. Academy uniform requires 20 min for cutting the fabric, 1hr for doing the stitching and 15 min for stitching the buttons and the button holes. The T.M. High School uniform requires 30 min, 1hrs and 30 min, respectively, for the same activities.
Q. Hi-Choice Dressers has the option to hire one more employee of any category. Whom should it hire to get the maximum increase in the production capacity, assuming that it needs to stitch only A.R. Academy uniforms on that day?
When they work alone, B needs 25% more time to nish a job than A does. They two nish the job in 13 days in the following manner: A works alone till half the job is done, then A and B work together for four days, and nally B works alone to complete the remaining 5% of the job. In how many days can B alone nish the entire job?





















