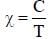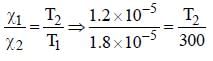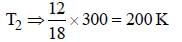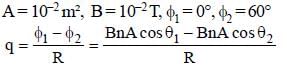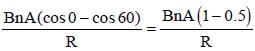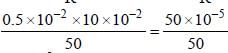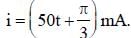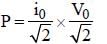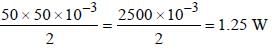Test: BITSAT Past Year Paper- 2014 - JEE MCQ
30 Questions MCQ Test - Test: BITSAT Past Year Paper- 2014
A rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface and fires 10 shots horizontally. Each bullet has a mass 10 g and a muzzle velocity of 800 ms–1. The velocity which the rifle man attains after firing 10 shots is
A train accelerating uniformly from rest attains a maximum speed of 40 ms–1 in 20 s. It travels at the speed for 20 s and is brought to rest with uniform retardation in further 40 s. What is the average velocity during the period ?
A projectile is fired with a velocity u making an angle q with the horizontal. What is the magnitude of change in velocity when it is at the highest point –
For the equation F = Aavbdc, where F is the force, A is the area, v is the velocity and d is the density, the values of a, b and c are respectively
A person with his hand in his pocket is skating on ice at the rate of 10m/s and describes a circle of radius 50 m. What is his inclination to vertical: (g = 10 m/sec2)
A small block of mass m is kept on a rough inclined surface of inclination q fixed in a elevator. The elevator goes up with a uniform velocity v and the block does not slide on the wedge. The work done by the force of friction on the block in time t will be :
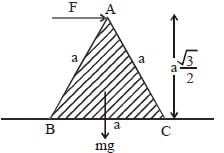
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction µ.
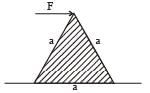
A horizontal force F is applied on the prism as shown in the figure.
If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is –
A spherically symmetric gravitational system of particles has a mass density 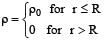 where r0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed V as a function of distance r (0 < r < ∞) from the centre of the system is represented by
where r0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed V as a function of distance r (0 < r < ∞) from the centre of the system is represented by
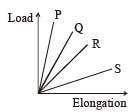
The load versus elongation graph for four wires is shown. The thinnest wire is
Th e wor k done in blowin g a soap bubble of surface tension 0.06 × Nm–1 from 2 cm radius to 5 cm radius is
The wavelength of radiation emitted by a body depends upon
One mole of O2 gas having a volume equal to 22.4 Litres at 0°C and 1 atmospheric pressure in compressed isothermally so that its volume reduces to 11.2 litres. The work done in this process is
In a thermodynamic process, the pressure of a fixed mass of a gas is changed in such a manner that the gas releases 20 J of heat and 8 J of work is done on the gas. If the initial internal energy of the gas was 30 J, then the final internal energy will be
In the kinetic theory of gases, which of these statements is/are true ?
(i) The pressure of a gas is proportional to the mean speed of the molecules.
(ii) The root mean square speed of the molecules is proportional to the pressure.
(iii) The rate of diffusion is proportional to the mean speed of the molecules.
(iv) The mean translational kinetic energy of a gas is proportional to its kelvin temperature.
Two balloons are filled one with pure he gas and other with air respectively. If the pressure and temperature of these balloons are same, then the number of molecules per unit volume is
Two particles P and Q describe S.H.M. of same amplitude a, same frequency f along the same straight line. The maximum distance between the two particles is a√2 . The initial phase difference between the particle is –
A tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
A soun d source, em itting sound of con stan t frequency, moves with a constant speed and crosses a stationary observer. The frequency (n) of sound heard by the observer is plotted against time (t). Which of the following graphs represents the correct variation ?
When a string is divided into three segments of length l1, l2, and l3 the fundamental frequencies of these three segments are v1, v2 and v3 respectively. The original fundamental frequency (v) of the string is
Two point dipoles pkˆ and p/2 kˆ are located at(0, 0, 0) and (1m, 0, 2m) respectively. The resultant electric field due to the two dipoles at the point (1m, 0, 0) is
Electric field in the region is given by 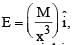 then the correct expression for the potential in the region is [assume potential at infinity is zero]
then the correct expression for the potential in the region is [assume potential at infinity is zero]
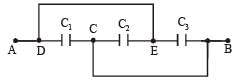
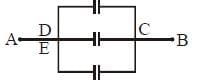
Three capacitors C1 = 1 µF, C2 = 2 µF and C3 = 3 µF are connected as shown in figure, then the equivalent capacitance between points A and B is
Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity s and a constant potential difference V is maintained between them, by a battery. Then the current, per unit length of the cylinder flowing from one cylinder to the other is –
A wire X is half the diameter and half the length of a wire Y of similar material. The ratio of resistance of X to that of Y is
A narrow beam of protons and deuterons, each having the same momentum, enters a region of uniform magnetic field directed perpendicular to their direction of momentum. The ratio of the radii of the circular paths described by them is
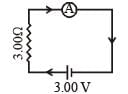
For th e cir cuit (figur e), the cur rent is to be measured. The ammeter shown is a galvanometer with a resistance RG = 60.00W converted to an ammeter by a shunt resistance rs = 0.02W. The value of the current is
The susceptibility of a magnetism at 300 K is 1.2 × 10–5. The temperature at which the susceptibility increases to 1.8 × 10–5 is
A coil 10 turns and a resistance of 20W is connected in series with B.G. of resistance 30W. The coil is placed with its plane perpendicular to the direction of a uniform magnetic field of induction 10–2 T. If it is now turned through an angle of 60° about an axis in its plane. Find the charge induced in the coil. (Area of a coil = 10–2 m²)
Voltage V and current i in AC circuit are given by V = 50 sin (50 t) volt, i = 50 sin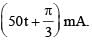 . The power dissipated in the circuit is
. The power dissipated in the circuit is
Resolving power of the telescope will be more, if the diameter of the objective is



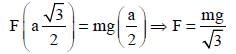
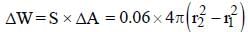
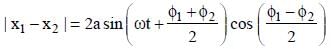
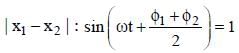
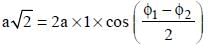
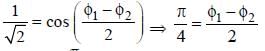
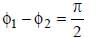
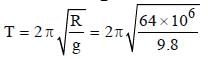
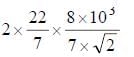
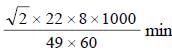
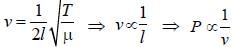
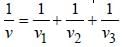
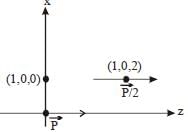
 dipole so that field at given point.
dipole so that field at given point.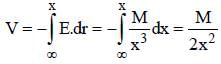

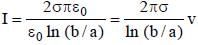
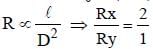
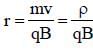
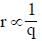
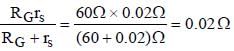 Total resistance in the circuit = 0.02 + 3
Total resistance in the circuit = 0.02 + 3