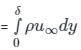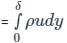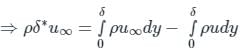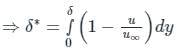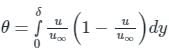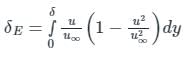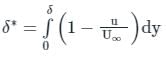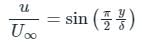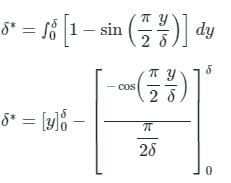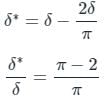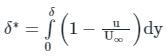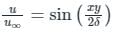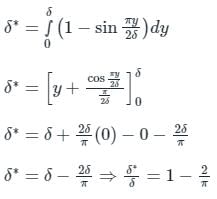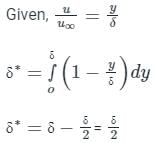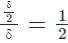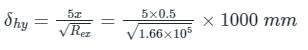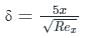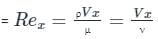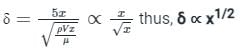Test: Boundary Layer Thickness - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Boundary Layer Thickness
δ*, δE and θ represents the displacement, Energy and momentum thickness then which of the following relation is correct.
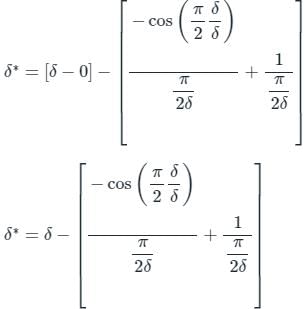
The velocity profile inside a boundary layer is given below u/U∞ = sin(πy/2δ). Then the value of (δ∗/δ) is:
The velocity profile inside the boundary layer for flow over a flat plate is given as 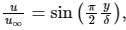 Where U∞ is the free stream velocity, δ is the local boundary layer thickness. If δ* is the local displacement thickness, the value of δ*/δ is
Where U∞ is the free stream velocity, δ is the local boundary layer thickness. If δ* is the local displacement thickness, the value of δ*/δ is
For a liner distribution of velocity profile in the laminar boundary layer on a flat plate given by u/U∞ = y/δ, the ratio of displacement thickness (δ*) to the boundary layer thickness (δ) is
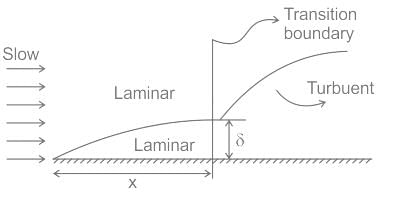
The nominal thickness of the boundary layer is defined when the velocity reaches the velocity of the free stream by
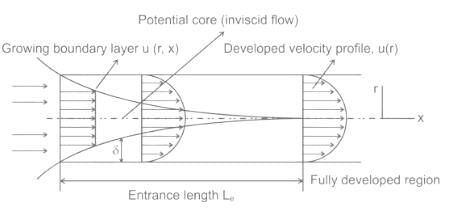
The maximum thickness of the boundary layer in a pipe of radius R is
A fluid (Prandtl number, Pr = 1) at 500 K flows over a flat plate of 1.5 m length, maintained at 300 K. The velocity of the fluid is 10 m/s. Assuming kinematic viscosity, v = 30 × 10-6 m2/s, the thermal boundary layer thickness (in mm) at 0.5 m from the leading edge is _________
The thickness of laminar boundary layer at a distance 'x' from the leading edge over a flat plate varies as: