Test: CAT Logical Reasoning & Data Interpretation- 7 - CAT MCQ
20 Questions MCQ Test - Test: CAT Logical Reasoning & Data Interpretation- 7
Directions: Read the information carefully and answer the question that follows.
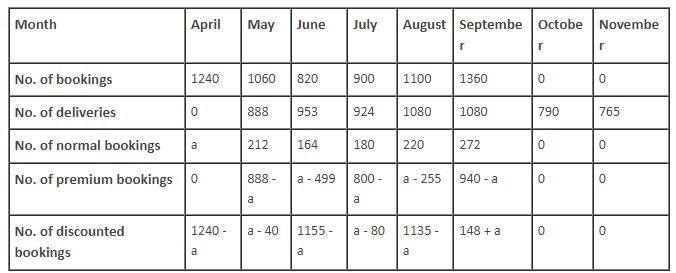
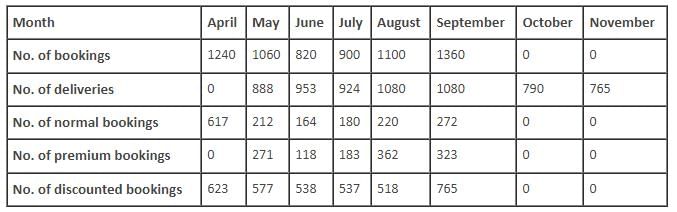
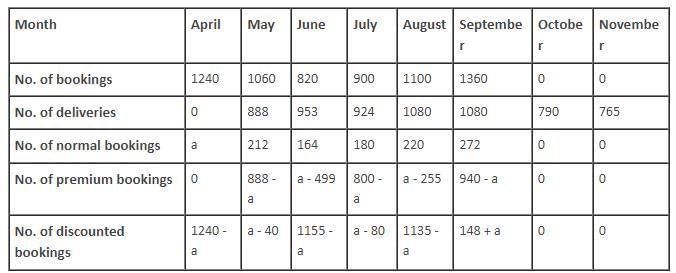
Apple launched its tablet i-pad on April 1, 2010. For the tablet, which was sold exclusively online, the bookings started on April 1, 2010 and ended on September 30, 2010. There was only 1 model in the entire line up and it was offered at a fixed price. There were 3 modes of booking. Premium booking (product delivered in the same month at 5% premium), i.e. one had to pay 105% of the price of the tablet.
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount, i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.
In every month, except April, exactly 1/5th of the bookings were normal bookings.
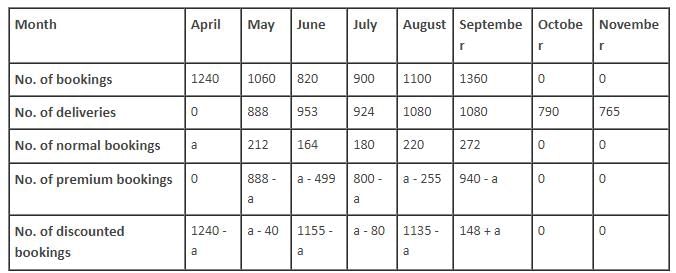
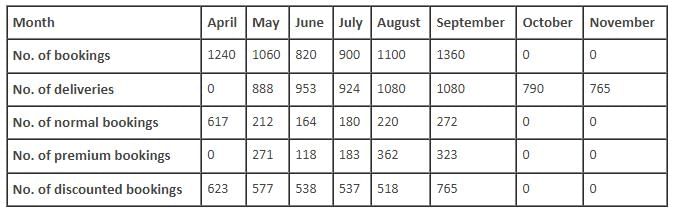
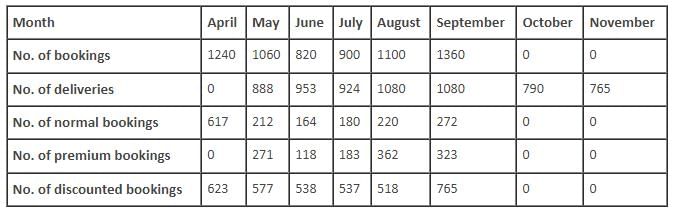
The following table gives the number of bookings and the number of deliveries for the given period.
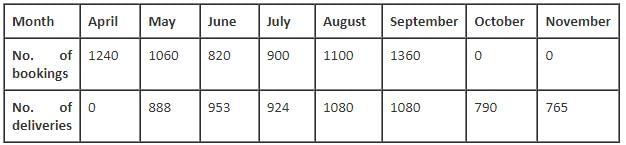
Q. What is the number of discounted bookings of tablets in May?
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount, i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.

Q. What is the number of discounted bookings of tablets in May?
Directions: Read the information carefully and answer the question that follows.
Apple launched its tablet i-pad on April 1, 2010. For the tablet, which was sold exclusively online, the bookings started on April 1, 2010 and ended on September 30, 2010. There was only 1 model in the entire line up and it was offered at a fixed price. There were 3 modes of booking. Premium booking (product delivered in the same month at 5% premium), i.e. one had to pay 105% of the price of the tablet.
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount, i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.
In every month, except April, exactly 1/5th of the bookings were normal bookings.
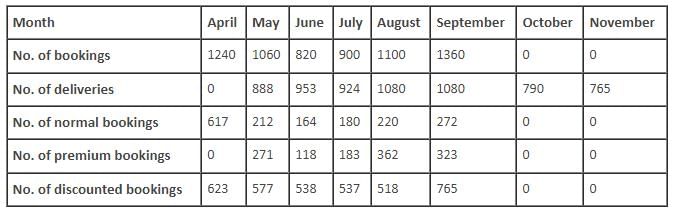
The following table gives the number of bookings and the number of deliveries for the given period.
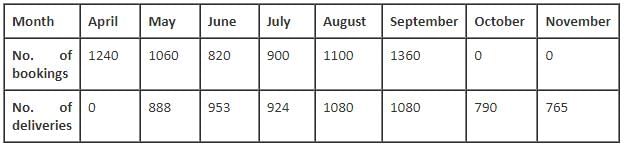
Q. In which month was there the highest increase in premium bookings of tablets as compared to the the previous month?
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount, i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.

Q. In which month was there the highest increase in premium bookings of tablets as compared to the the previous month?
Directions: Read the information carefully and answer the question that follows.
Apple launched its tablet i-pad on April 1, 2010. For the tablet, which was sold exclusively online, the bookings started on April 1, 2010 and ended on September 30, 2010. There was only 1 model in the entire line up and it was offered at a fixed price. There were 3 modes of booking. Premium booking (product delivered in the same month at 5% premium), i.e. one had to pay 105% of the price of the tablet.
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount, i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.
In every month, except April, exactly 1/5th of the bookings were normal bookings.
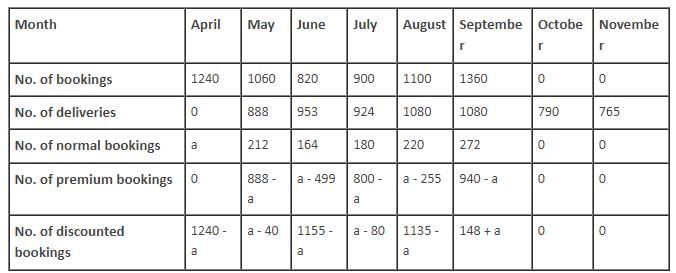
The following table gives the number of bookings and the number of deliveries for the given period.
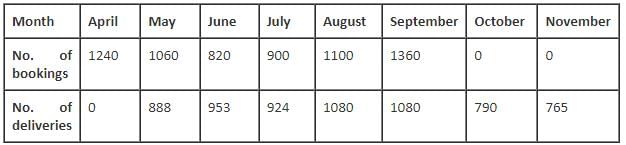
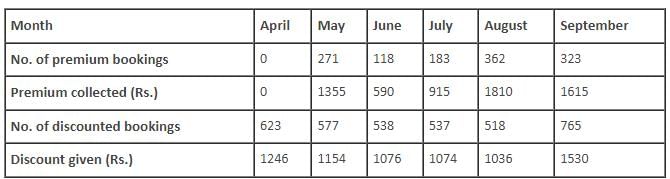
Q. For how many months was the premium collected more than the discount given?
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount, i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.

Q. For how many months was the premium collected more than the discount given?
Directions: Read the information carefully and answer the question that follows.
Apple launched its tablet i-pad on April 1, 2010. For the tablet, which was sold exclusively online, the bookings started on April 1, 2010 and ended on September 30, 2010. There was only 1 model in the entire line up and it was offered at a fixed price. There were 3 modes of booking. Premium booking (product delivered in the same month at 5% premium), i.e. one had to pay 105% of the price of the tablet.
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.
In every month, except April, exactly 1/5th of the bookings were normal bookings.
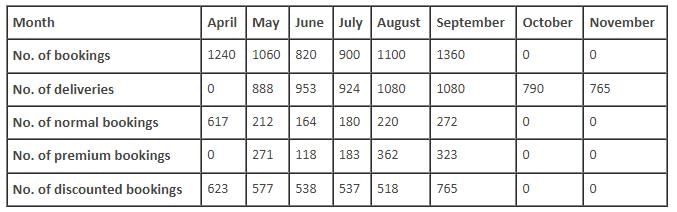
The following table gives the number of bookings and the number of deliveries for the given period.
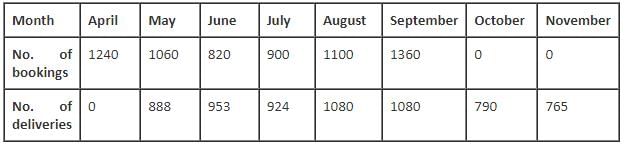
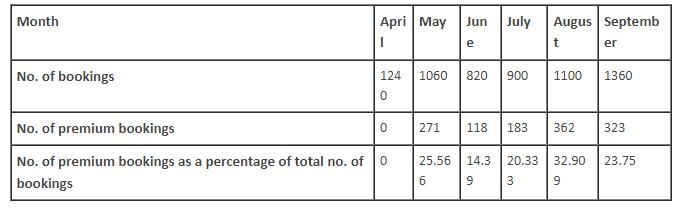
Q. In which of the following months was the number of premium bookings as a percentage of total bookings the highest?
Directions: Read the information carefully and answer the question that follows.
Apple launched its tablet i-pad on April 1, 2010. For the tablet, which was sold exclusively online, the bookings started on April 1, 2010 and ended on September 30, 2010. There was only 1 model in the entire line up and it was offered at a fixed price. There were 3 modes of booking. Premium booking (product delivered in the same month at 5% premium), i.e. one had to pay 105% of the price of the tablet.
Normal booking (product delivered in the next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 1)th month, without any extra charge.
Discounted booking (product delivered in next to next month), i.e. if the booking was done in the nth month, it was delivered in the (n + 2)th month, at 2% discount i.e. one had to pay 98% of the price of the tablet. The payment for all kind of deliveries was done in the month of the booking.
In every month, except April, exactly 1/5th of the bookings were normal bookings.
The following table gives the number of bookings and the number of deliveries for the given period.
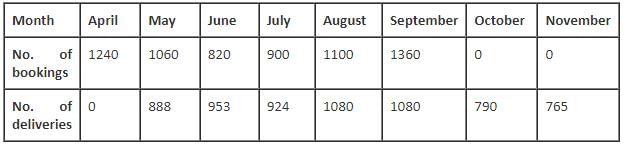
Q. How many tablets booked in June were delivered in August?
Directions: Read the given information carefully and answer the question that follows.
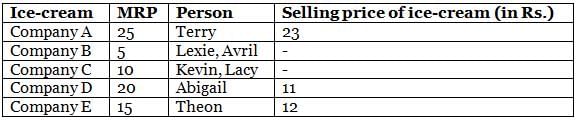
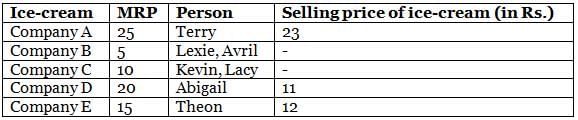
Mr. Webster has an ice-cream shop, where he sells ice creams of different companies (Company A, Company B, Company C, Company D and Company E). The maximum price at which he can sell an ice-cream is called MRP (Maximum Retail Price). The MRP for each of the five ice-cream service companies is a distinct value, such as Rs. 5, Rs. 10, Rs. 15, Rs. 20 and Rs. 25, not necessarily in that order. On a particular day, Mr. Webster sold exactly seven ice-creams, each to a different customer. The customers were Abigail, Avril, Kevin, Lacy, Lexie, Terry and Theon.
The following information is known about the ice-creams that he sold.
(1) He sold at least one ice-cream from each ice-cream company.
(2) The MRP of ice-cream of Company A is greater than Rs. 15, but he did not sell ice-cream of Company A to Avril.
(3) He sold two ice-creams, one to Kevin and one to Lacy, of the same ice-cream company of MRP Rs. 10.
(4) He sold Company D ice-cream to Abigail for Rs. 11 and the maximum selling price of any ice-cream that he sold to any of the seven customers was Rs. 23.
(5) He sold the ice-cream with MRP of Rs. 15 only to Theon.
(6) He sold two ice-creams of Company B, one of which was to Lexie and sold ice-cream of Company E for Rs. 12.
Q. Mr. Webster sold an ice-cream of Company B to which of the following customers?
Directions: Read the given information carefully and answer the question that follows.
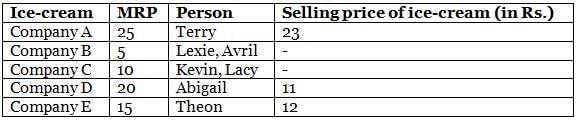
Mr. Webster has an ice-cream shop, where he sells ice creams of different companies (Company A, Company B, Company C, Company D and Company E). The maximum price at which he can sell an ice-cream is called MRP (Maximum Retail Price). The MRP for each of the five ice-cream service companies is a distinct value, such as Rs. 5, Rs. 10, Rs. 15, Rs. 20 and Rs. 25, not necessarily in that order. On a particular day, Mr. Webster sold exactly seven ice-creams, each to a different customer. The customers were Abigail, Avril, Kevin, Lacy, Lexie, Terry and Theon.
The following information is known about the ice-creams that he sold.
(1) He sold at least one ice-cream from each ice-cream company.
(2) The MRP of ice-cream of Company A is greater than Rs. 15, but he did not sell ice-cream of Company A to Avril.
(3) He sold two ice-creams, one to Kevin and one to Lacy, of the same ice-cream company of MRP Rs. 10.
(4) He sold Company D ice-cream to Abigail for Rs. 11 and the maximum selling price of any ice-cream that he sold to any of the seven customers was Rs. 23.
(5) He sold the ice-cream with MRP of Rs. 15 only to Theon.
(6) He sold two ice-creams of Company B, one of which was to Lexie and sold ice-cream of Company E for Rs. 12.
Q. What is the MRP(in Rs.) of Company E's ice-cream?
Directions: Read the given information carefully and answer the question that follows.
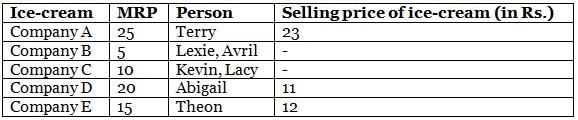
Mr. Webster has an ice-cream shop, where he sells ice creams of different companies (Company A, Company B, Company C, Company D and Company E). The maximum price at which he can sell an ice-cream is called MRP (Maximum Retail Price). The MRP for each of the five ice-cream service companies is a distinct value, such as Rs. 5, Rs. 10, Rs. 15, Rs. 20 and Rs. 25, not necessarily in that order. On a particular day, Mr. Webster sold exactly seven ice-creams, each to a different customer. The customers were Abigail, Avril, Kevin, Lacy, Lexie, Terry and Theon.
The following information is known about the ice-creams that he sold.
(1) He sold at least one ice-cream from each ice-cream company.
(2) The MRP of ice-cream of Company A is greater than Rs. 15, but he did not sell ice-cream of Company A to Avril.
(3) He sold two ice-creams, one to Kevin and one to Lacy, of the same ice-cream company of MRP Rs. 10.
(4) He sold Company D ice-cream to Abigail for Rs. 11 and the maximum selling price of any ice-cream that he sold to any of the seven customers was Rs. 23.
(5) He sold the ice-cream with MRP of Rs. 15 only to Theon.
(6) He sold two ice-creams of Company B, one of which was to Lexie and sold ice-cream of Company E for Rs. 12.
Q. Mr. Webster sold two ice-creams of which of the following companies to two different customers?
Directions: Read the given information carefully and answer the question that follows.
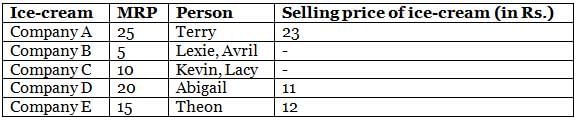
Mr. Webster has an ice-cream shop, where he sells ice creams of different companies (Company A, Company B, Company C, Company D and Company E). The maximum price at which he can sell an ice-cream is called MRP (Maximum Retail Price). The MRP for each of the five ice-cream service companies is a distinct value, such as Rs. 5, Rs. 10, Rs. 15, Rs. 20 and Rs. 25, not necessarily in that order. On a particular day, Mr. Webster sold exactly seven ice-creams, each to a different customer. The customers were Abigail, Avril, Kevin, Lacy, Lexie, Terry and Theon.
The following information is known about the ice-creams that he sold.
(1) He sold at least one ice-cream from each ice-cream company.
(2) The MRP of ice-cream of Company A is greater than Rs. 15, but he did not sell ice-cream of Company A to Avril.
(3) He sold two ice-creams, one to Kevin and one to Lacy, of the same ice-cream company of MRP Rs. 10.
(4) He sold Company D ice-cream to Abigail for Rs. 11 and the maximum selling price of any ice-cream that he sold to any of the seven customers was Rs. 23.
(5) He sold the ice-cream with MRP of Rs. 15 only to Theon.
(6) He sold two ice-creams of Company B, one of which was to Lexie and sold ice-cream of Company E for Rs. 12.
Q. What can be the maximum selling price (in Rs.) of the ice-cream that Mr. Webster sold to Avril?
Directions: Read the given information carefully and answer the question that follows.
Mr. Webster has an ice-cream shop, where he sells ice creams of different companies (Company A, Company B, Company C, Company D and Company E). The maximum price at which he can sell an ice-cream is called MRP (Maximum Retail Price). The MRP for each of the five ice-cream service companies is a distinct value, such as Rs. 5, Rs. 10, Rs. 15, Rs. 20 and Rs. 25, not necessarily in that order. On a particular day, Mr. Webster sold exactly seven ice-creams, each to a different customer. The customers were Abigail, Avril, Kevin, Lacy, Lexie, Terry and Theon.
The following information is known about the ice-creams that he sold.
(1) He sold at least one ice-cream from each ice-cream company.
(2) The MRP of ice-cream of Company A is greater than Rs. 15, but he did not sell ice-cream of Company A to Avril.
(3) He sold two ice-creams, one to Kevin and one to Lacy, of the same ice-cream company of MRP Rs. 10.
(4) He sold Company D ice-cream to Abigail for Rs. 11 and the maximum selling price of any ice-cream that he sold to any of the seven customers was Rs. 23.
(5) He sold the ice-cream with MRP of Rs. 15 only to Theon.
(6) He sold two ice-creams of Company B, one of which was to Lexie and sold ice-cream of Company E for Rs. 12.
Q. What is the difference between the MRPs (in Rs.) of ice creams sold to Abigail and Terry?
Directions: Read the information given below and answer the question that follows.
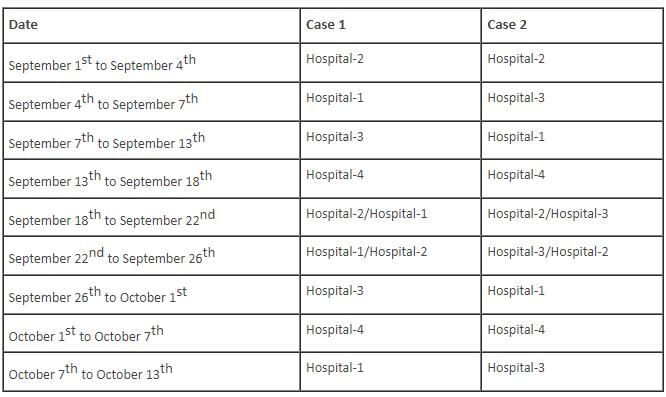
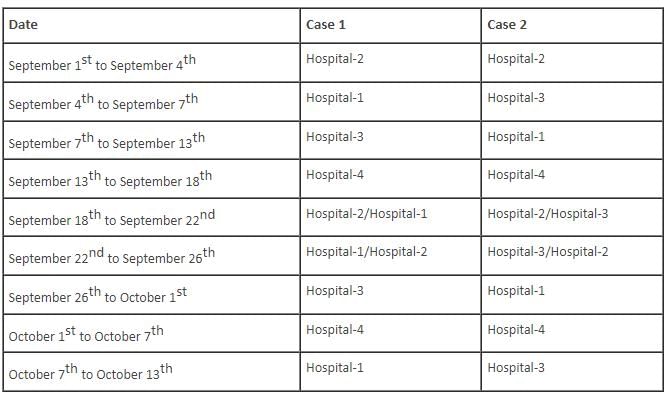
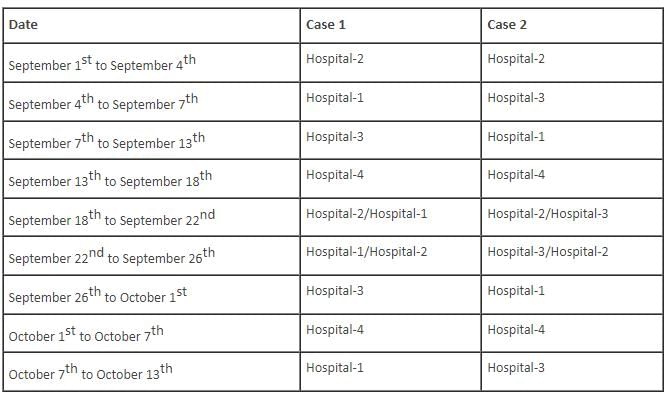
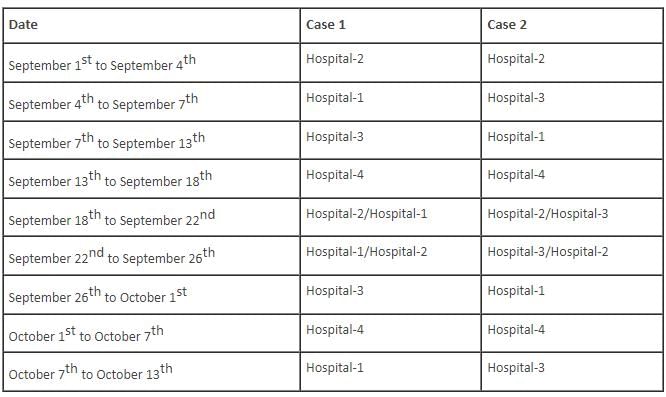
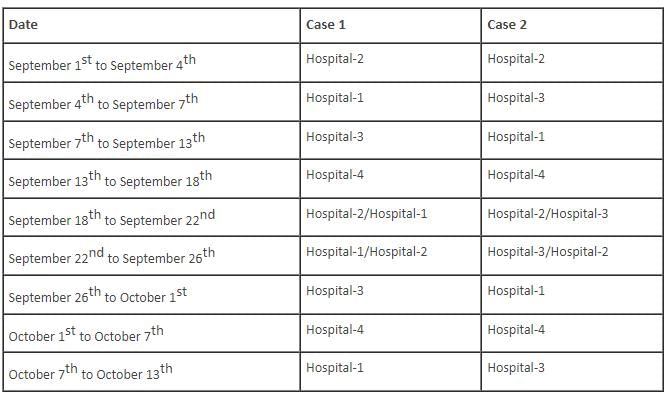
Mr. Smith, a renowned neurosurgeon, works in four different hospitals – Hospital-1, Hospital-2, Hospital-3 and Hospital-4, situated in different cities. When travelling between any two hospitals, he always travels by car. Further, journey between any two hospitals is completed in one day. Also, if he starts a journey from any hospital on a day, he reaches that hospital again only after at least ten days. Last year, on September 1, Mr. Smith reached Hospital-2 from Hospital-4. During the months of September and October of that year, Mr. Smith travelled only on September 4, September 7, September 13, September 18, September 22, September 26, October 1, October 7 and October 13. On October 13, he reached Hospital-2. The number of days that he stayed in any hospital does not include the day on which he reached that hospital and the day on which he started a journey from that hospital.
Q. For how many days did Mr. Smith stay in Hospital-2, during the period September 1st to October 13th?
Directions: Read the information given below and answer the question that follows.
Mr. Smith, a renowned neurosurgeon, works in four different hospitals – Hospital-1, Hospital-2, Hospital-3 and Hospital-4, situated in different cities. When travelling between any two hospitals, he always travels by car. Further, journey between any two hospitals is completed in one day. Also, if he starts a journey from any hospital on a day, he reaches that hospital again only after at least ten days. Last year, on September 1, Mr. Smith reached Hospital-2 from Hospital-4. During the months of September and October of that year, Mr. Smith travelled only on September 4, September 7, September 13, September 18, September 22, September 26, October 1, October 7 and October 13. On October 13, he reached Hospital-2. The number of days that he stayed in any hospital does not include the day on which he reached that hospital and the day on which he started a journey from that hospital.
Q. For how many days did Mr. Smith stay in Hospital-1, during the period September 1st to October 13th?
Directions: Read the information given below and answer the question that follows.
Mr. Smith, a renowned neurosurgeon, works in four different hospitals – Hospital-1, Hospital-2, Hospital-3 and Hospital-4, situated in different cities. When travelling between any two hospitals, he always travels by car. Further, journey between any two hospitals is completed in one day. Also, if he starts a journey from any hospital on a day, he reaches that hospital again only after at least ten days. Last year, on September 1, Mr. Smith reached Hospital-2 from Hospital-4. During the months of September and October of that year, Mr. Smith travelled only on September 4, September 7, September 13, September 18, September 22, September 26, October 1, October 7 and October 13. On October 13, he reached Hospital-2. The number of days that he stayed in any hospital does not include the day on which he reached that hospital and the day on which he started a journey from that hospital.
Q. If Mr. Smith stayed in Hospital-3 on September 19, in which hospital did Mr. Smith stay on October 10?
Directions: Read the information given below and answer the question that follows.
Mr. Smith, a renowned neurosurgeon, works in four different hospitals – Hospital-1, Hospital-2, Hospital-3 and Hospital-4, situated in different cities. When travelling between any two hospitals, he always travels by car. Further, journey between any two hospitals is completed in one day. Also, if he starts a journey from any hospital on a day, he reaches that hospital again only after at least ten days. Last year, on September 1, Mr. Smith reached Hospital-2 from Hospital-4. During the months of September and October of that year, Mr. Smith travelled only on September 4, September 7, September 13, September 18, September 22, September 26, October 1, October 7 and October 13. On October 13, he reached Hospital-2. The number of days that he stayed in any hospital does not include the day on which he reached that hospital and the day on which he started a journey from that hospital.
Q. Which of the following cannot be the origin and destination Mr. Smith took during the period from September 1 to October 13?
Directions: Read the information given below and answer the question that follows.
Mr. Smith, a renowned neurosurgeon, works in four different hospitals – Hospital-1, Hospital-2, Hospital-3 and Hospital-4, situated in different cities. When travelling between any two hospitals, he always travels by car. Further, journey between any two hospitals is completed in one day. Also, if he starts a journey from any hospital on a day, he reaches that hospital again only after at least ten days. Last year, on September 1, Mr. Smith reached Hospital-2 from Hospital-4. During the months of September and October of that year, Mr. Smith travelled only on September 4, September 7, September 13, September 18, September 22, September 26, October 1, October 7 and October 13. On October 13, he reached Hospital-2. The number of days that he stayed in any hospital does not include the day on which he reached that hospital and the day on which he started a journey from that hospital.
Q. Mr. Smith stayed in which of the following hospitals on September 22?
Directions: Answer the question on the basis of the information given below.
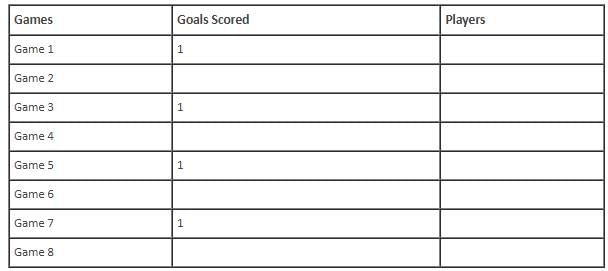
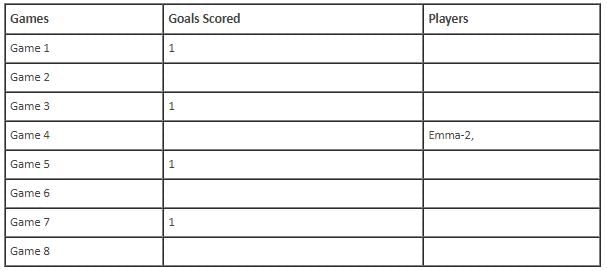
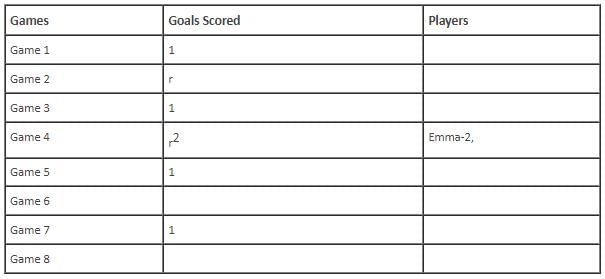
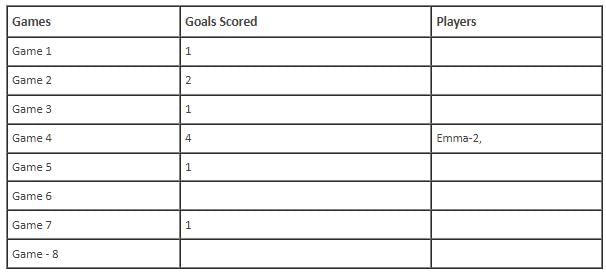
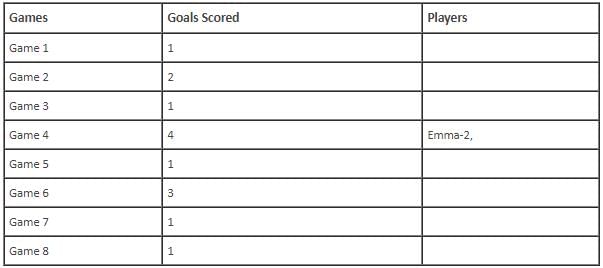
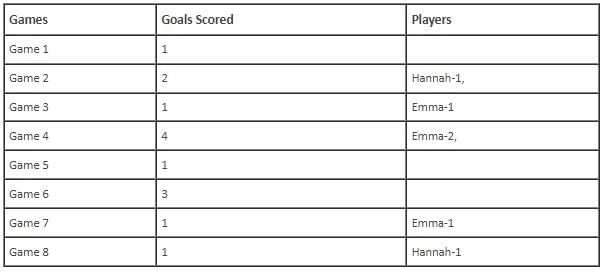
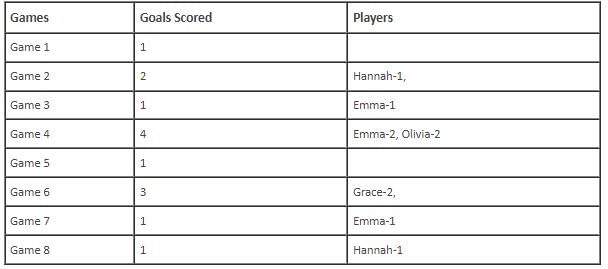
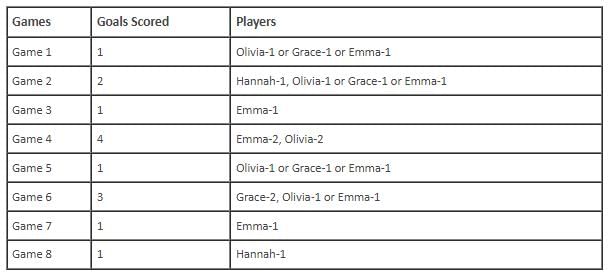
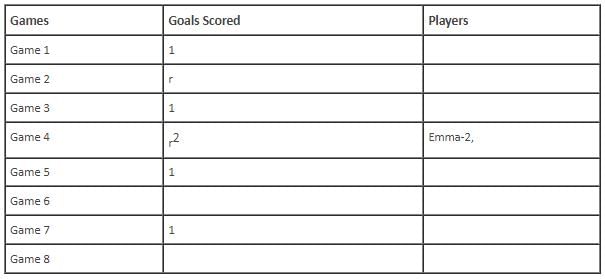
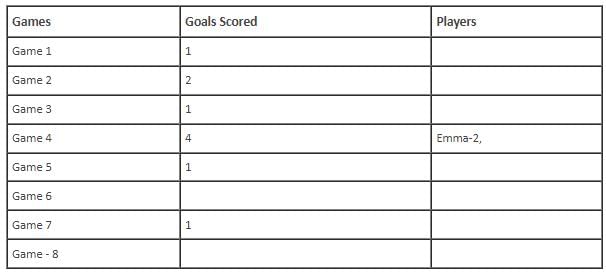
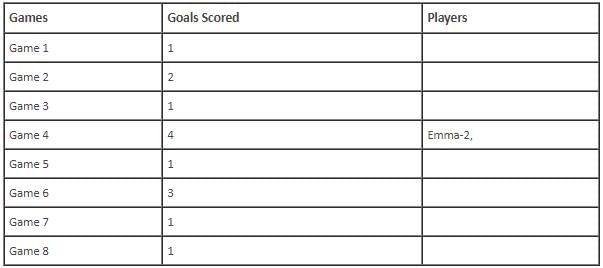
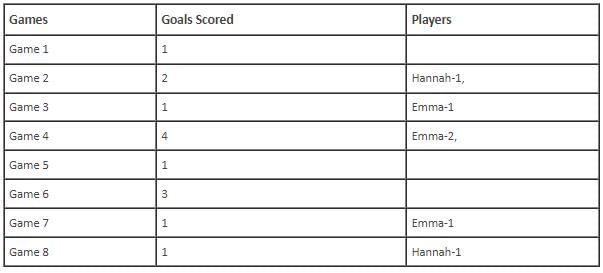
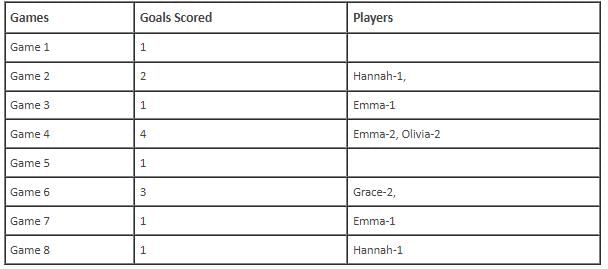
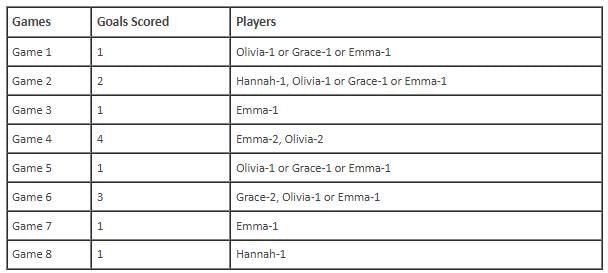
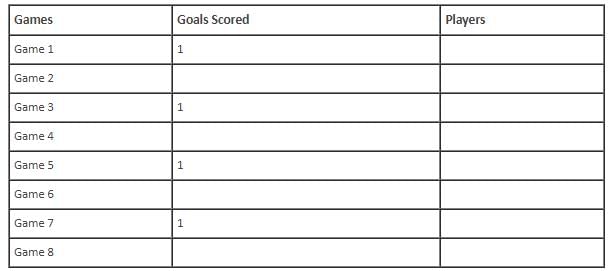
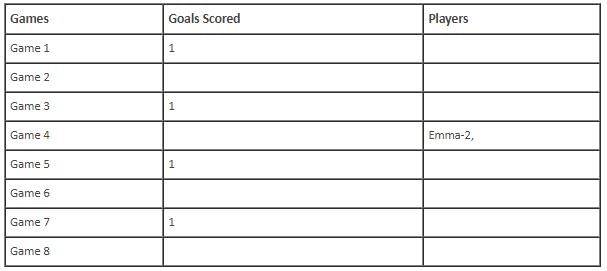
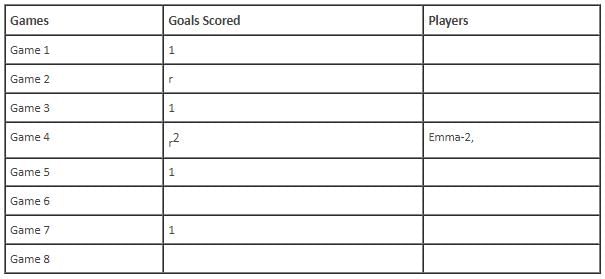
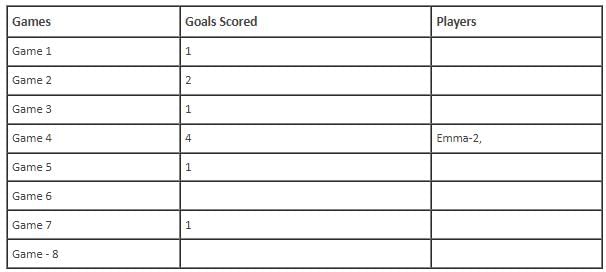
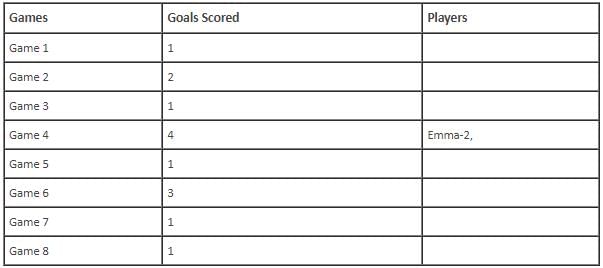
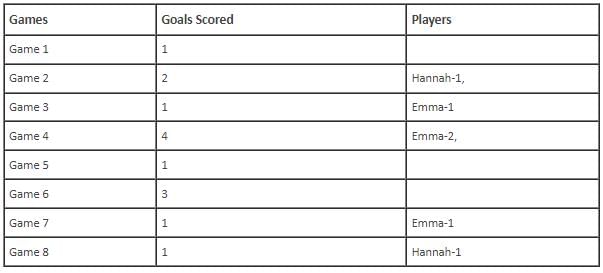
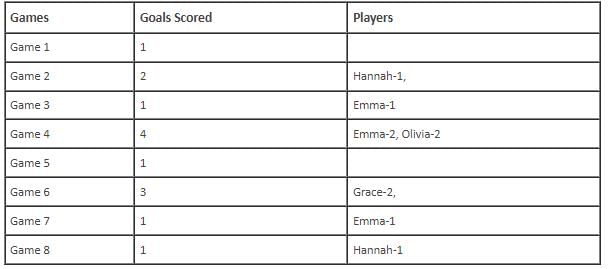
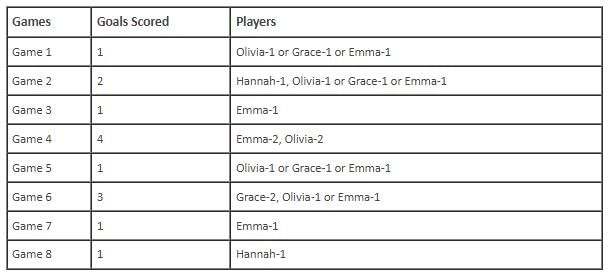
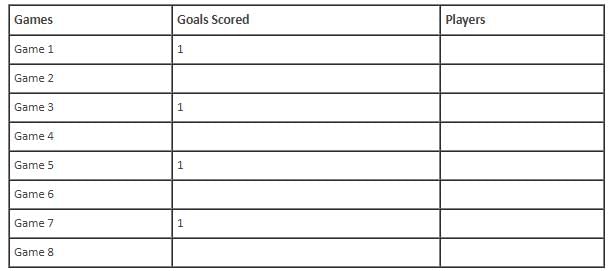
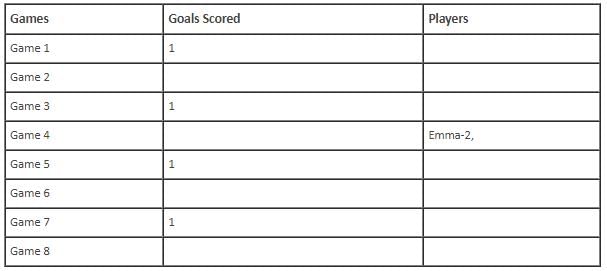
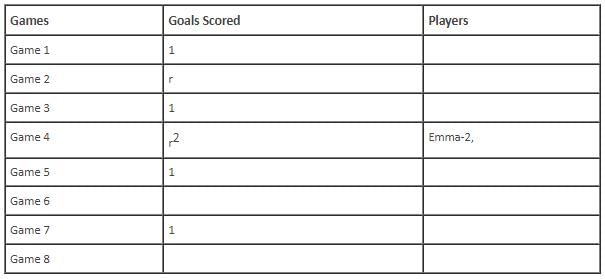
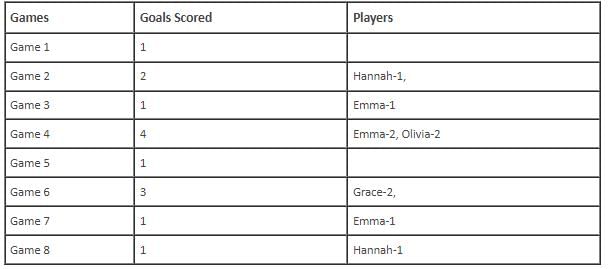
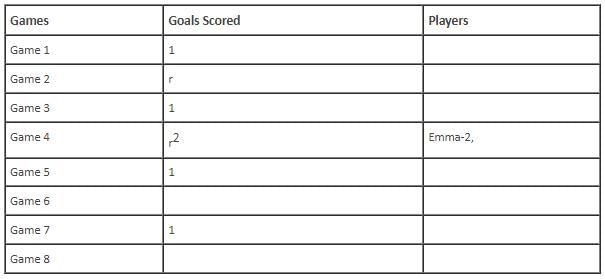
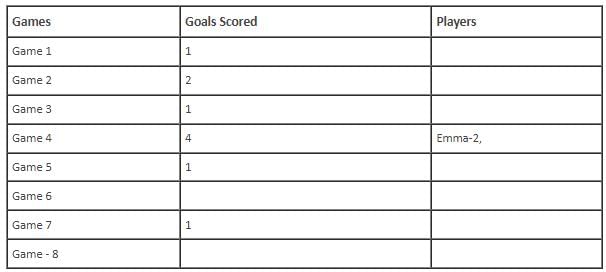
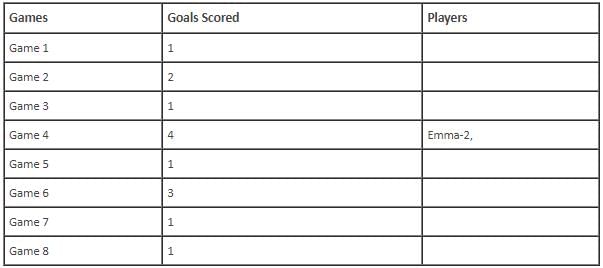
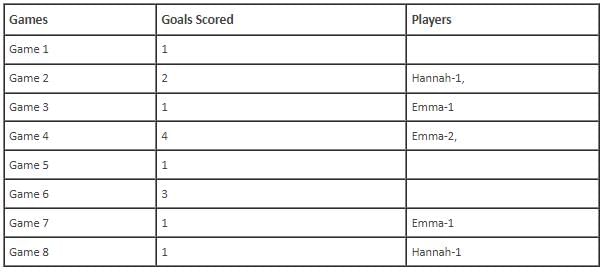
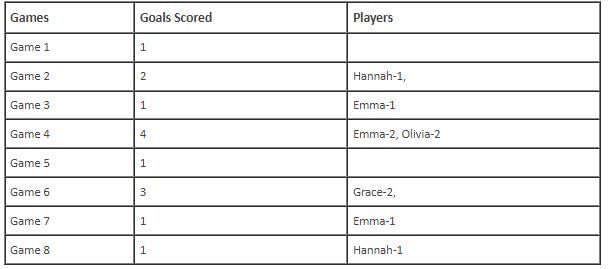
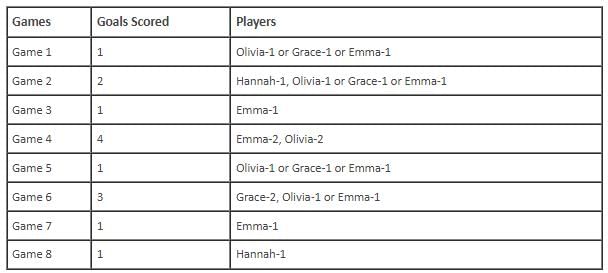
In the evaluation process for a professional football team, the coaching staff meticulously assessed the performance of four talented women players: Emma, Grace, Hannah, and Olivia. The team management aimed to determine their eligibility and potential selection for the upcoming season. To make informed decisions, the coaching staff analysed the players' scoring records from the past 8 games, labelled as Game 1 through Game 8. Collectively, the four players had scored a total of 14 goals across these games. Notably, each player had contributed by scoring at least two goal, showcasing their individual contributions to the team's success. Additionally, no two players had the same total number of goals. Several key facts emerged from the analysis of these players' scoring records.
(i) Surprisingly, only one goal was scored in every odd-numbered game.
(ii) Emma scored 2 goals in Game 4 and emerged as a dominant scorer, surpassing Grace in terms of the number of goals scored.
(iii) The player with the highest number of goals achieved this feat scoring in exactly four games, including Game 3 and Game 7.
(iv) Hannah is known for her lowest scoring capabilities, and scored in Game 2 and Game 8. Furthermore, Olivia and Grace both scored 2 goals each in Game 4 and Game 6, respectively.
(v) Interestingly, goals scored in Game 1, Game 2 and Game 4 are in geometric progression (GP).
(vi) The second highest number of goals scored is unique and it is scored in Game 6.
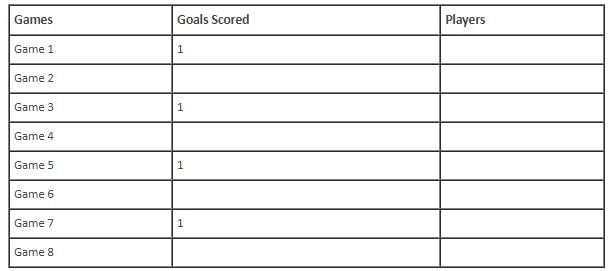
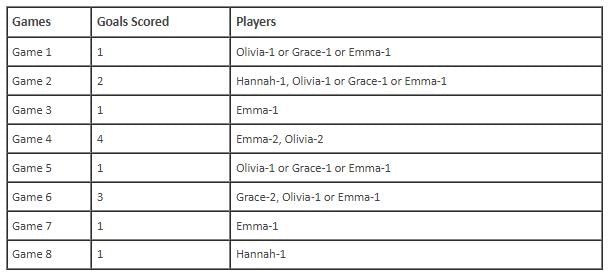
Q. Which of the following can be the possible player(s) who scored goal in Game 1?
Directions: Answer the question on the basis of the information given below.
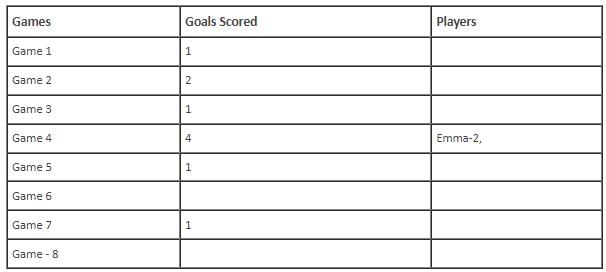
In the evaluation process for a professional football team, the coaching staff meticulously assessed the performance of four talented women players: Emma, Grace, Hannah, and Olivia. The team management aimed to determine their eligibility and potential selection for the upcoming season. To make informed decisions, the coaching staff analysed the players' scoring records from the past 8 games, labelled as Game 1 through Game 8. Collectively, the four players had scored a total of 14 goals across these games. Notably, each player had contributed by scoring at least two goal, showcasing their individual contributions to the team's success. Additionally, no two players had the same total number of goals. Several key facts emerged from the analysis of these players' scoring records.
(i) Surprisingly, only one goal was scored in every odd-numbered game.
(ii) Emma scored 2 goals in Game 4 and emerged as a dominant scorer, surpassing Grace in terms of the number of goals scored.
(iii) The player with the highest number of goals achieved this feat scoring in exactly four games, including Game 3 and Game 7.
(iv) Hannah is known for her lowest scoring capabilities, and scored in Game 2 and Game 8. Furthermore, Olivia and Grace both scored 2 goals each in Game 4 and Game 6, respectively.
(v) Interestingly, goals scored in Game 1, Game 2 and Game 4 are in geometric progression (GP).
(vi) The second highest number of goals scored is unique and it is scored in Game 6.
Q. What is the maximum possible number of games in which Olivia scored goal? Key in the value.
Directions: Answer the question on the basis of the information given below.
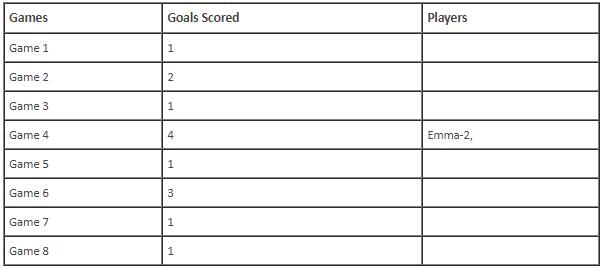
In the evaluation process for a professional football team, the coaching staff meticulously assessed the performance of four talented women players: Emma, Grace, Hannah, and Olivia. The team management aimed to determine their eligibility and potential selection for the upcoming season. To make informed decisions, the coaching staff analysed the players' scoring records from the past 8 games, labelled as Game 1 through Game 8. Collectively, the four players had scored a total of 14 goals across these games. Notably, each player had contributed by scoring at least two goal, showcasing their individual contributions to the team's success. Additionally, no two players had the same total number of goals. Several key facts emerged from the analysis of these players' scoring records.
(i) Surprisingly, only one goal was scored in every odd-numbered game.
(ii) Emma scored 2 goals in Game 4 and emerged as a dominant scorer, surpassing Grace in terms of the number of goals scored.
(iii) The player with the highest number of goals achieved this feat scoring in exactly four games, including Game 3 and Game 7.
(iv) Hannah is known for her lowest scoring capabilities, and scored in Game 2 and Game 8. Furthermore, Olivia and Grace both scored 2 goals each in Game 4 and Game 6, respectively.
(v) Interestingly, goals scored in Game 1, Game 2 and Game 4 are in geometric progression (GP).
(vi) The second highest number of goals scored is unique and it is scored in Game 6.
Q. For how many games is the number of goals scored less than the number of goals scored in Game 8? Key in the value.
Directions: Answer the question on the basis of the information given below.
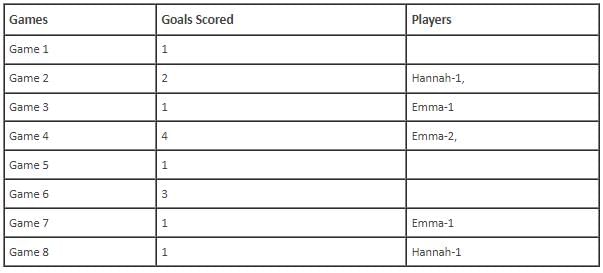
In the evaluation process for a professional football team, the coaching staff meticulously assessed the performance of four talented women players: Emma, Grace, Hannah, and Olivia. The team management aimed to determine their eligibility and potential selection for the upcoming season. To make informed decisions, the coaching staff analysed the players' scoring records from the past 8 games, labelled as Game 1 through Game 8. Collectively, the four players had scored a total of 14 goals across these games. Notably, each player had contributed by scoring at least two goal, showcasing their individual contributions to the team's success. Additionally, no two players had the same total number of goals. Several key facts emerged from the analysis of these players' scoring records.
(i) Surprisingly, only one goal was scored in every odd-numbered game.
(ii) Emma scored 2 goals in Game 4 and emerged as a dominant scorer, surpassing Grace in terms of the number of goals scored.
(iii) The player with the highest number of goals achieved this feat scoring in exactly four games, including Game 3 and Game 7.
(iv) Hannah is known for her lowest scoring capabilities, and scored in Game 2 and Game 8. Furthermore, Olivia and Grace both scored 2 goals each in Game 4 and Game 6, respectively.
(v) Interestingly, goals scored in Game 1, Game 2 and Game 4 are in geometric progression (GP).
(vi) The second highest number of goals scored is unique and it is scored in Game 6.
Consider the following statements:
(i) The sum of goals scored in Game 6, Game 7 and Game 8 is equal to the sum of goals scored in Game 4 and Game 5.
(ii) The second highest number of goals scored is 2.
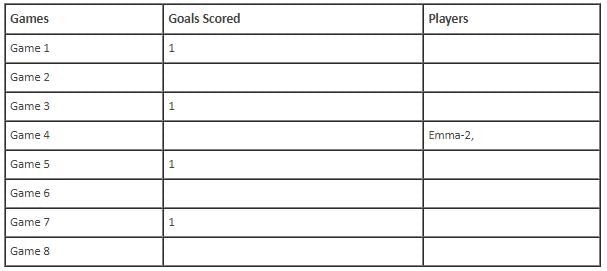
Q. Which of the above statements is/are correct?
Directions: Answer the question on the basis of the information given below.
In the evaluation process for a professional football team, the coaching staff meticulously assessed the performance of four talented women players: Emma, Grace, Hannah, and Olivia. The team management aimed to determine their eligibility and potential selection for the upcoming season. To make informed decisions, the coaching staff analysed the players' scoring records from the past 8 games, labelled as Game 1 through Game 8. Collectively, the four players had scored a total of 14 goals across these games. Notably, each player had contributed by scoring at least two goal, showcasing their individual contributions to the team's success. Additionally, no two players had the same total number of goals. Several key facts emerged from the analysis of these players' scoring records.
(i) Surprisingly, only one goal was scored in every odd-numbered game.
(ii) Emma scored 2 goals in Game 4 and emerged as a dominant scorer, surpassing Grace in terms of the number of goals scored.
(iii) The player with the highest number of goals achieved this feat scoring in exactly four games, including Game 3 and Game 7.
(iv) Hannah is known for her lowest scoring capabilities, and scored in Game 2 and Game 8. Furthermore, Olivia and Grace both scored 2 goals each in Game 4 and Game 6, respectively.
(v) Interestingly, goals scored in Game 1, Game 2 and Game 4 are in geometric progression (GP).
(vi) The second highest number of goals scored is unique and it is scored in Game 6.
Consider the following statements:
(i) The sum of goals scored in Game 6, Game 7 and Game 8 is equal to the sum of goals scored in Game 4 and Game 5.
(ii) The second highest number of goals scored is 2.
Q. If Emma scored goal in Game 1, then which of following groups of players scored goals in Game 6?