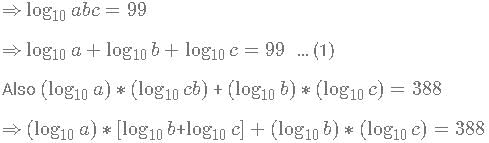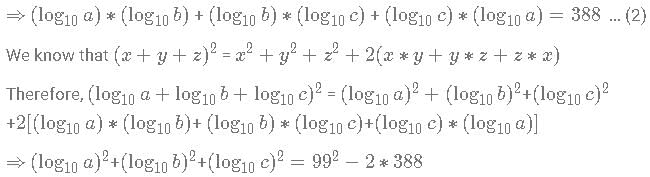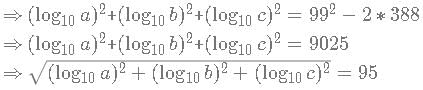Test: CAT Quantitative Aptitude- 2 - CAT MCQ
22 Questions MCQ Test - Test: CAT Quantitative Aptitude- 2
Ramesh went to a food joint and bought some burgers and rolls for his family members. In total, he spent less than Rs. 3000. Had Ramesh spent the amount he actually spent on buying burgers to buy rolls and vice versa, he would have ended up buying 3 more items in total. What is the maximum number of burgers that Ramesh could have bought if it is known that a burger and a roll cost Rs. 80 and Rs. 60 respectively?
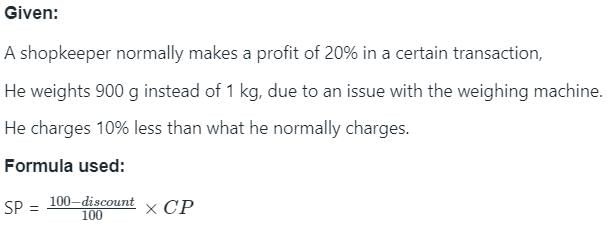
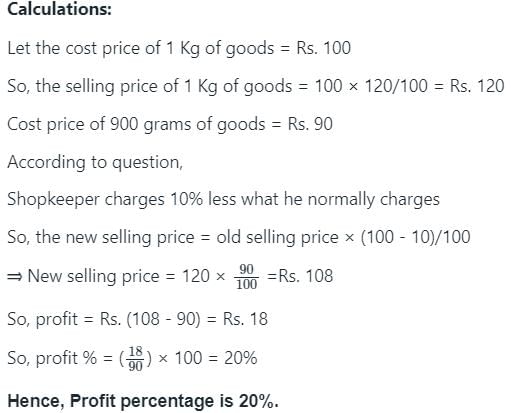
A shopkeeper normally makes a profit of 20% in a certain transaction; he weights 900 g instead of 1 kg, due to an issue with the weighing machine. If he charges 10% less than what he normally charges, what is his actual profit or loss percentage?
Virat, Rohit and Shikhar finished as the top 3 run scorers in IPL 2018. Virat scored half the number of runs scored by Rohit and Shikhar combined whereas Rohit scored one-fourth of what Virat and Shikar scored together. If Virat scored 150 runs more than Rohit, then the total runs scored by the 3 players is
Set P has 4 elements and set Q has 5 elements. How many numbers of functions are defined from P to Q?
We are told that f(x) is a polynomial function such that f(a)f(b) = f(a) + f(b) + f(ab) - 2 and f(4) = 17, find the value of f(7).
If N = 823 - 623 - 203, then N can be expressed as a product of ________ with 3
A distinct number of contracts were given to each of the nine major construction companies. Find the least number of contracts that could have been given to the company that got the lowest number of contracts among the nine companies, such that sum of the number of contracts given to any five companies is greater than the sum of number of contracts given to the remaining four companies.
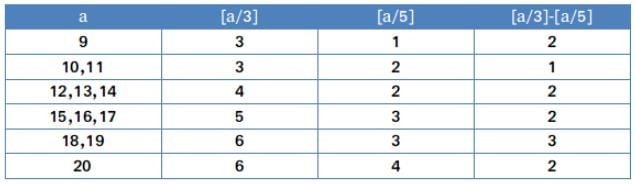
If [X] represents the greatest integer function, a is a positive integer where [a/3]-[a/5]=2 then what is the number of possible values a can take?
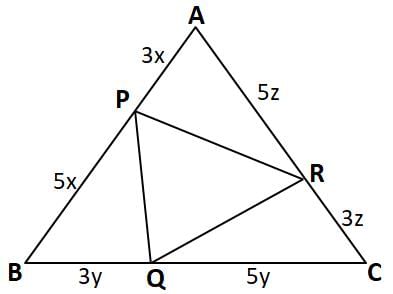
In a △ABC, three points P, Q and R lie on sides AB, BC and CA respectively such that AP : PB = BQ:QC = CR:RA = 3:5. Find out the ratio of the area of \triangle△PQR to that of △ABC.
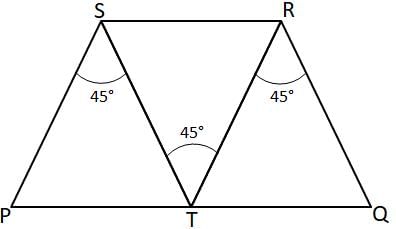
In a quadilateral PQRS, T is a point on the side PQ such that \angle∠PST = \angle∠STR = \angle∠TRQ = 45°. If PS = 16 cm and RQ = 24 cm then find out the area of triangle TRS?
A wire which was used to form a square of side 30 cm is divided into 3 parts such that the length of the longest part is 25% more than length of the second longest part. If the shortest part is 20 cm shorter than the longest part, then the area (in cm2) of the triangle formed by these three parts is
When the number of sides of a polygon increases from 'n' to 'n+1', A is the change in the sum of exterior angles and B is the change in the sum of interior angles. Which of the following statements is true?
For any point, in the first quadrant, on the line 4x + 9y = 36, what is the maximum value of x6 * y6 ?
Find the area of the region enclosed between the lines y=2|x|+3 and y=-2|x|+8.
If it is known that xx and yy are two positive numbers such that 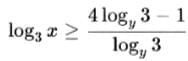 what is the minimum value of x + y ?
what is the minimum value of x + y ?
If log m=300×log1.0033333..
What is the approximate value of m?
Three positive numbers a, b and c are such that 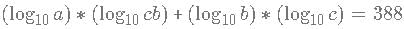 and abc = 1099. Find the value of
and abc = 1099. Find the value of 
N is a multiple of 72. Also, it is known that all the digits of N are different. What is the largest possible value of N?
The number of ways in which 33 identical pens can be distributed among three boys such that each of them receives an odd number of pens is
A shopkeeper has 5 dozens of apples. On selling 12 apples for Rs.600, he incurs a loss equal to the cost price of 2 apples. At what total price should he mark the remaining 4 dozens so that even after giving 20% discount, he would have an overall gain of 10%?
An investor is faced with a dilemma about where to invest his savings of 10 lakhs. Scheme A gives 10% interest compounded annually for 2 years and simple interest of 20% for the next 3 years. If the amount has increased less than 60%, additional 10% is also added to it. Scheme B gives a simple interest of 10% for 2 years and compound interest of 20% for 3 years compounded annually. If the amount has increased less than 50%, additional 15% is added to it. If the investor goes with the right choice, how much does he earn over his initial investment ?
An infinite geometric progression has the sum 10. Sum of all the possible integral values of the first term is




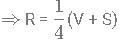

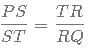
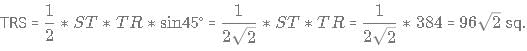 cm
cm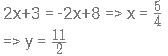

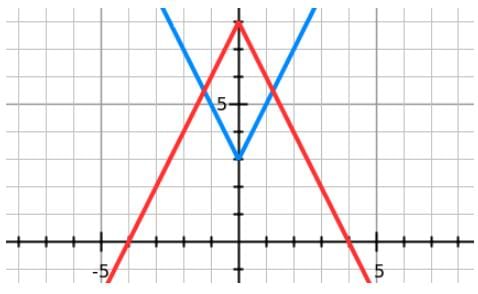
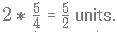
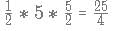 square units.
square units.