CUET Commerce Exam > CUET Commerce Tests > General Test Preparation for CUET UG > Test: Calendar 3 - CUET Commerce MCQ
Test: Calendar 3 - CUET Commerce MCQ
Test Description
20 Questions MCQ Test General Test Preparation for CUET UG - Test: Calendar 3
Test: Calendar 3 for CUET Commerce 2025 is part of General Test Preparation for CUET UG preparation. The Test: Calendar 3 questions and answers have been
prepared according to the CUET Commerce exam syllabus.The Test: Calendar 3 MCQs are made for CUET Commerce 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Calendar 3 below.
Solutions of Test: Calendar 3 questions in English are available as part of our General Test Preparation for CUET UG for CUET Commerce & Test: Calendar 3 solutions in
Hindi for General Test Preparation for CUET UG course. Download more important topics, notes, lectures and mock
test series for CUET Commerce Exam by signing up for free. Attempt Test: Calendar 3 | 20 questions in 20 minutes | Mock test for CUET Commerce preparation | Free important questions MCQ to study General Test Preparation for CUET UG for CUET Commerce Exam | Download free PDF with solutions
Detailed Solution for Test: Calendar 3 - Question 1
Detailed Solution for Test: Calendar 3 - Question 2
Test: Calendar 3 - Question 3
01-Jan-2007 was Monday. What day of the week lies on 01-Jan-2008?
Detailed Solution for Test: Calendar 3 - Question 3
Test: Calendar 3 - Question 4
1.12.91 is the first Sunday. Which is the fourth Tuesday of December 91?
Detailed Solution for Test: Calendar 3 - Question 4
Detailed Solution for Test: Calendar 3 - Question 5
Detailed Solution for Test: Calendar 3 - Question 6
Test: Calendar 3 - Question 7
How many odd days are there from 13th May, 2005 to 19th August 2005 (both inclusive)?
Detailed Solution for Test: Calendar 3 - Question 7
Test: Calendar 3 - Question 8
What is the year next to 1990 which will have the same calendar as that of the year 1990?
Detailed Solution for Test: Calendar 3 - Question 8
Detailed Solution for Test: Calendar 3 - Question 9
Detailed Solution for Test: Calendar 3 - Question 10
Test: Calendar 3 - Question 11
How many days are there from 3rd February, 2012 to 18th April 2012 (both inclusive)?
Detailed Solution for Test: Calendar 3 - Question 11
Detailed Solution for Test: Calendar 3 - Question 12
Detailed Solution for Test: Calendar 3 - Question 13
Detailed Solution for Test: Calendar 3 - Question 14
Detailed Solution for Test: Calendar 3 - Question 15
Detailed Solution for Test: Calendar 3 - Question 16
Detailed Solution for Test: Calendar 3 - Question 17
Detailed Solution for Test: Calendar 3 - Question 18
Test: Calendar 3 - Question 19
The year next to 2005 will have the same calendar as that of the year 2005?
Detailed Solution for Test: Calendar 3 - Question 19
Test: Calendar 3 - Question 20
If Feb 12th,1986 falls on Wednesday then Jan 1st,1987 falls on which day?
Detailed Solution for Test: Calendar 3 - Question 20
|
164 videos|607 docs|942 tests
|
Information about Test: Calendar 3 Page
In this test you can find the Exam questions for Test: Calendar 3 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Calendar 3, EduRev gives you an ample number of Online tests for practice


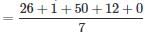

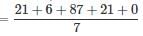
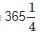 days-by about 11 minutes. To compensate for this discrepancy, the leap year is omitted three times every four hundred years.
days-by about 11 minutes. To compensate for this discrepancy, the leap year is omitted three times every four hundred years.











