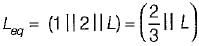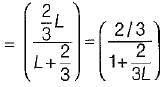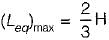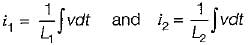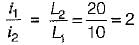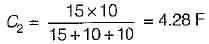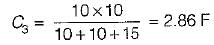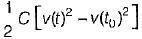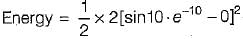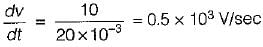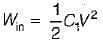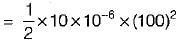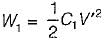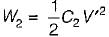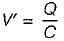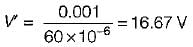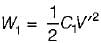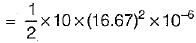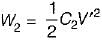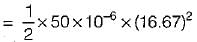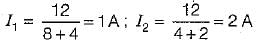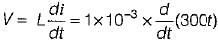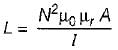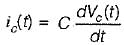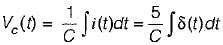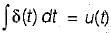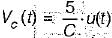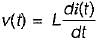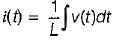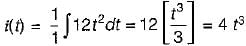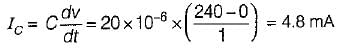Test: Capacitors & Inductors- 2 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Capacitors & Inductors- 2
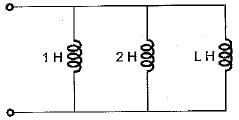
There inductances, 1 H, 2 H and L H are in parallel. The maximum value of equivalent inductance will be
Figure given below shows a parallel combination of 10 mH and 20 mH inductances in parallel. A time varying voltage is applied across the inductances at any time instant and the total current supplied by the time varying source is 25 amps.
The values of instantaneous currents through each of the inductances are given by
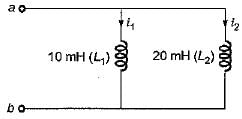
The values of instantaneous currents through each of the inductances are given by

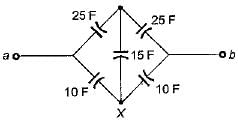
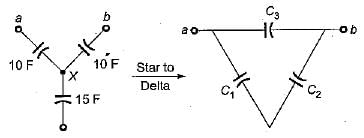
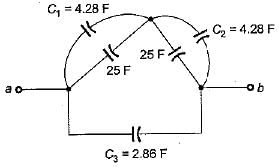
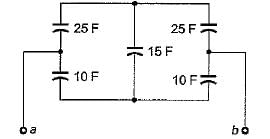
The equivalent capacitance between the terminals a-b for the capacitive circuit shown below is

A voltage v(t) = e-t sin t is connected to a capacitance C = 2 F. The energy stored in the capacitor for t = 0 to t = 10 sec is
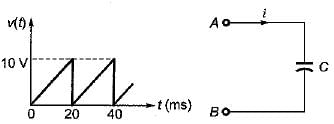
A sawtooth voltage as shown in figure below is applied between the terminals A-B to a capacitor of C = 30 μF. The current i will be
Assertion (A): In steady state condition, the energy consumed is infinite for both inductor and capacitor.
Reason (R): The current i in the capacitor and voltage v\n the inductor are zero in steady state.
Assertion (A): If the voltage across the capacitor being constant, current through it is zero.
Reason (R): On application of dc voltage and with no initial charge, the capacitor first acts as short circuit but as soon as the full charge it retains, the capacitor behaves as open circuit.
A 10 μF capacitor is charged full by 100 V dc source. It is then connected across an uncharged capacitor of 50 μF capacity. The energy stored in the two capacitors in the final state will be
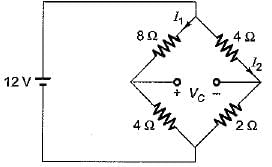
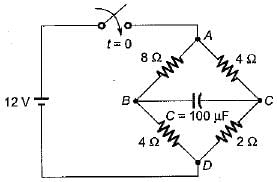
For the bridge circuit shown below, the charge accumulated in the capacitor under steady state condition is
A current of i = 300t is suddenly applied to an inductance of 1 mH. The induced voltage will be
A 100-turn coil has an inductance of 6 mH. if the number of turns is increased by 200%, all other quantities remaining the same, the inductance will be
A current input,5 δ(t) is flow through a capacitor C. The voltage VC(t), across capacitor is given by
A voltage waveform v(t) = 12 t2 is applied across1 H inductor for t > 0 with initial current through it being zero. The current through the inductor for t > 0 is given by
Which of the following statements associated with capacitor is wrong?
Potential difference across a capacitor of capacitance of 20 μF is increased uniformly from 0 to 240 V in 1 second. The charging current will be
Assertion (A): Lower the self inductance of a coil more the delay in establishing steady current through it.
Reason (R): An inductor opposes a sudden change in current.
Consider the following statements regarding an inductor:
1. An inductor is a sort of short circuit to dc.
2. An inductor is a sort of open circuit to dc.
3. An inductor never dissipates energy but only stores it.
4. A finite amount of energy can be stored in an inductor even if voltage across it is zero, such as when the current through it is constant.
Q. Which of the above statements is/are not correct?
Assertion (A): A capacitor can store charge.
Reason (R): The plates of the condenser are conductive.
Assertion (A): It is impossible to change the current through an inductor by finite amount in zero time.
Reason (R): The current through an inductor can be changed by finite amount in zero time only when an infinite voltage is applied across it.