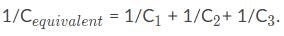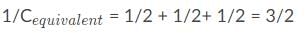Test: Capacitors - MCAT MCQ
10 Questions MCQ Test Physics for MCAT - Test: Capacitors
In a parallel-plate capacitor, how can the capacitance be decreased?
Imagine a parallel-plate capacitor with a plate separation of d = 1 cm. The plates are both right triangles with both base and height equal to 2 cm. What is the capacitance of this capacitor? (assume 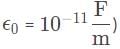
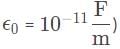
A parallel plate capacitor separated 10 cm, by an air barrier is connected to a 100 V battery. The capacitance of the capacitor is 1 picofarad while the battery is connected. Without disconnecting the battery, the parallel plates are moved so they are now 20 cm apart. What happens to the energy stored in the capacitor?
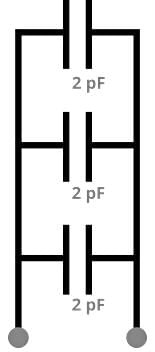
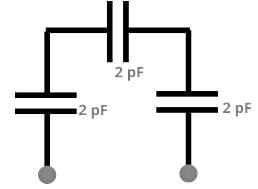
What is the correct order of the capacitances of these circuits, from lowest to highest? Assume all capacitors have the same capacitance.
If you are given a large parallel-plate capacitor containing just air as a dielectric, which of the following tools would be sufficient to determine the capacitor’s capacitance?
Which of the following parallel plate capacitors will store the most charge on the positive plate when a potential difference V is applied across the plate?
Four capacitors of 10 pF are connected in parallel with two of the capacitors having a Mylar dielectric (κ = 3) of thickness L inserted and two capacitors only separated by air at a distance L. A voltage potential of 40 V is applied across the circuit. How does the charge stored on the capacitors differ between the capacitors with the Mylar and without?
Four capacitors of 10 pF are connected in parallel with two of the capacitors having a Mylar dielectric (κ = 3) of thickness L inserted and two capacitors only separated by air at a distance L. A voltage potential of 40 V is applied across the circuit and subsequently disconnected. The Mylar dielectrics are then removed and charges are allowed to equilibrate in the system. What is the energy stored on each capacitor?
|
158 videos|9 docs|21 tests
|


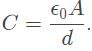
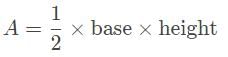
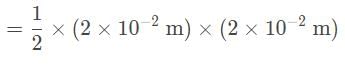
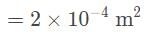
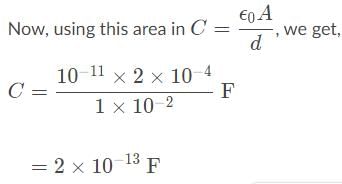

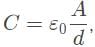 so substitute that in.
so substitute that in.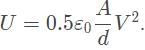 d increases from 10 cm to 20 cm.
d increases from 10 cm to 20 cm.