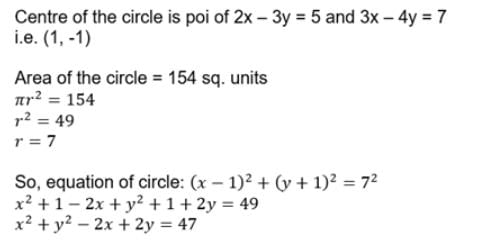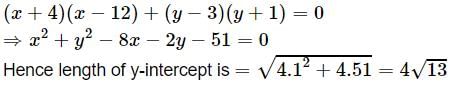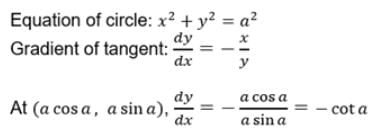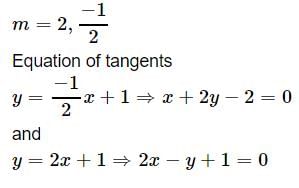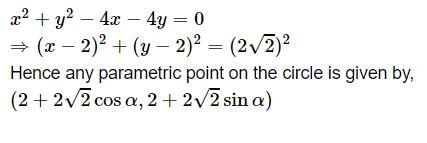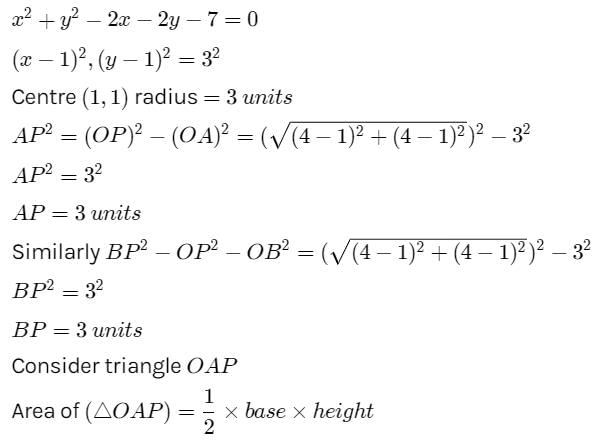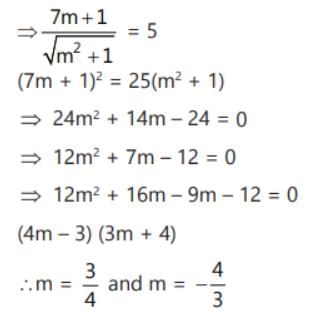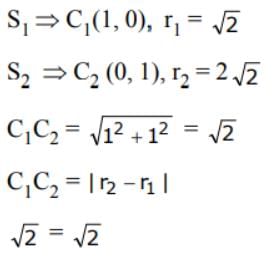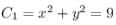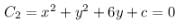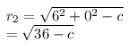Test: Circle- 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Circle- 2
The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. The equation of the circle is
If a be the radius of a circle which touches x-axis at the origin, then its equation is
The equation of the circle passing through (3, 6) and whose centre is (2, –1) is
The equation of a circle which passes through the three points (3, 0) (1, –6), (4, –1) is
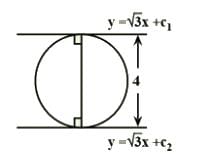
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
B and C are fixed point having co-ordinates (3, 0) and (–3, 0) respectively. If the vertical angle BAC is 90º, then the locus of the centroid of the DABC has the equation
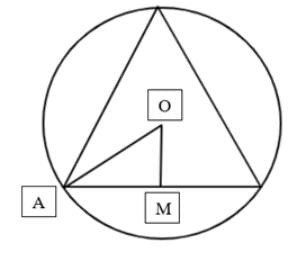
The area of an equilateral triangle inscribed in the circle x2 + y2 – 2x = 0 is
The length of intercept on y-axis, by a circle whose diameter is the line joining the points (–4,3) and (12,–1) is
The gradient of the tangent line at the point (a cos a, a sin a) to the circle x2 + y2 = a2, is
If y = c is a tangent to the circle x2+y2–2x+2y–2 = 0 at (1, 1), then the value of c is
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are
The greatest distance of the point P(10, 7) from the circle x2 + y2 – 4x – 2y – 20 = 0 is
The equation of the normal to the circle x2+y2 = 9 at the point is
The parametric coordinates of any point on the circle x2 + y2 – 4x – 4y = 0 are
The length of the tangent drawn from the point (2, 3) to the circles 2(x2 + y2) – 7x + 9y – 11 = 0.
Tangents are drawn from (4, 4) to the circle x2 + y2 – 2x – 2y – 7 = 0 to meet the circle at A and B. The length of the chord AB is
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals
Pair of tangents are drawn from every point on the line 3x + 4y = 12 on the circle x2+ y2 = 4. Their variable chord of contact always passes through a fixed point whose co-ordinates are
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is
The locus of the centres of the circles such that the point (2, 3) is the mid point of the chord 5x + 2y = 16 is
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is
A circle is drawn touching the x-axis and centre at the point which is the reflection of (a, b) in the line y – x = 0. The equation of the circle is
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0
The point from which the tangents to the circles x2 + y2 – 8x + 40 = 0, 5x2 + 5y2 – 25 x + 80 = 0, x2 + y2 – 8x + 16y + 160 = 0 are equal in length is
If the circle x2 + y2 = 9 touches the circle x2 + y2 + 6y + c = 0, then c is equal to
The tangent from the point of intersection of the lines 2x – 3y + 1 = 0 and 3x – 2y –1 = 0 to the circle x2 + y2 + 2x – 4y = 0 is
The length of the common chord of circles x2 + y2 – 6x – 16 = 0 and x2 + y2 – 8y – 9 = 0 is
The distance between the chords of contact of tangents to the circle x2 + y2 + 2gx + 2fy + c = 0 from the origin and from the point (g, f) is
|
209 videos|447 docs|187 tests
|
|
209 videos|447 docs|187 tests
|