Test: Circles- 2 - GMAT MCQ
6 Questions MCQ Test - Test: Circles- 2
If 1/a2 + a2 represents the diameter of circle O and 1/a + a = 3, which of the following best approximates the circumference of circle O?
Two circular road signs are to be painted yellow. If the radius of the larger sign is twice that of the smaller sign, how many times more paint is needed to paint the larger sign (assuming that a given amount of paint covers the same area on both signs)?
In the diagram, points A, B, and C are on the diameter of the circle with center B. Additionally, all arcs
pictured are semicircles. Suppose angle YXA = 105 degrees. What is the ratio of the area of the shaded region above the line YB to the area of the shaded region below the line YB? (Note: Diagram is not drawn to scale and angles drawn are not accurate.)
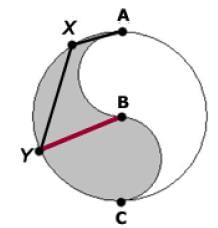
pictured are semicircles. Suppose angle YXA = 105 degrees. What is the ratio of the area of the shaded region above the line YB to the area of the shaded region below the line YB? (Note: Diagram is not drawn to scale and angles drawn are not accurate.)

Two circles share a center at point C, as shown. Segment AC is broken up into two shorter segments, AB and BC, with dimensions shown. What is the ratio of the area of the large circle to the area of the small circle?

The length of minor arc AB is twice the length of minor arc BC and the length of minor arc AC is three times the length of minor arc AB. What is the measure of angle BCA?
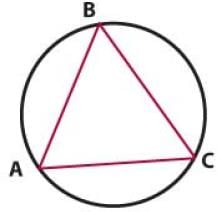
In the figure, circle O has center O, diameter AB and a radius of 5. Line CD is parallel to the diameter. What is the perimeter of the shaded region?



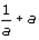 and
and 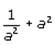 . If we square
. If we square 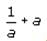
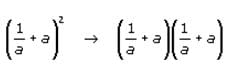
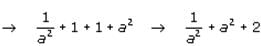 We can use this information to manipulate the equation
We can use this information to manipulate the equation 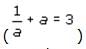 provided in the question. If we square both sides of the given equation, we arrive at the following:
provided in the question. If we square both sides of the given equation, we arrive at the following: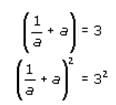
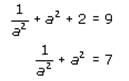
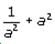 which we have determined is equal to 7.
which we have determined is equal to 7.

















