All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Tests  >  Class 9: Additional Practice  >  Test: Circles- Case Based Type Questions - Class 9 MCQ

Test: Circles- Case Based Type Questions - Class 9 MCQ


Test Description

12 Questions MCQ Test Class 9: Additional Practice - Test: Circles- Case Based Type Questions

Test: Circles- Case Based Type Questions for Class 9 2024 is part of Class 9: Additional Practice preparation. The Test: Circles- Case Based Type Questions questions and answers have been prepared according to the Class 9 exam syllabus.The Test: Circles- Case Based Type Questions MCQs are made for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Circles- Case Based Type Questions below.
Solutions of Test: Circles- Case Based Type Questions questions in English are available as part of our Class 9: Additional Practice for Class 9 & Test: Circles- Case Based Type Questions solutions in Hindi for Class 9: Additional Practice course. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free. Attempt Test: Circles- Case Based Type Questions | 12 questions in 24 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study Class 9: Additional Practice for Class 9 Exam | Download free PDF with solutions
Test: Circles- Case Based Type Questions - Question 1
Save

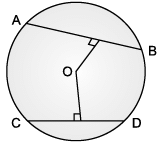
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. A quadrilateral is called cyclic if all the four vertices of it lie on a _________

Detailed Solution for Test: Circles- Case Based Type Questions - Question 1
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral.
Test: Circles- Case Based Type Questions - Question 2
Save

In a circle of radius 10 cm given below, chord AB and CD are equal. If OE bisects AB and OF bisects CD and OF = 6 cm, then length EB is ________ .

Detailed Solution for Test: Circles- Case Based Type Questions - Question 2

It is given AB = CD.

So, OF = OE = 6 cm [Equal chords are equidistant from centre] ...... (1)

In ΔOEB
OB = 10 cm [Radius]
OE = OF = 6 cm [from (1)]

Since a line through the center that bisects the chord is perpendicular to the chord, we must have ∠OBE=90∘
∴OB2 = OE2+EB2
[∵∠OEB is 90∘]

EB2=OB2−OE2

EB2 = (10)2−(6)2 = 64

EB = 8 cm

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Circles- Case Based Type Questions - Question 3
Save

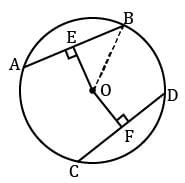
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. What is the length of AB?

Detailed Solution for Test: Circles- Case Based Type Questions - Question 3
Length of AB = 16 cm

h2 = p2 + b2

102 = 62 + b2

100 = 36 + b2

= 8 cm

AB = 8 + 8

= 16 cm

Test: Circles- Case Based Type Questions - Question 4
Save

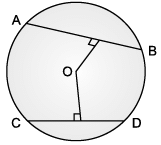
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. A circle divides the plane, on which it lies, in _________ parts.
Detailed Solution for Test: Circles- Case Based Type Questions - Question 4
parts (inside, outside and on the circle)
Test: Circles- Case Based Type Questions - Question 5
Save

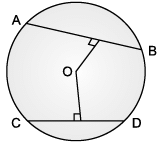
Rohan draws a circle of radius 10 cm with the help of compass and scale. He also draws two chords, AB and CD in such a way that AB and CD are 6 cm and 8 cm from the centre O. Now, he has some doubts that are given below. Help him out by answering these questions:

Q. Which statement is not true?

Detailed Solution for Test: Circles- Case Based Type Questions - Question 5
The sum of each pair of opposite angles of a cyclic quadrilateral is 90°.
Test: Circles- Case Based Type Questions - Question 6
Save

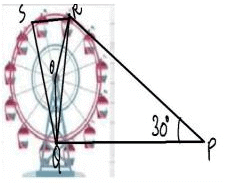
A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

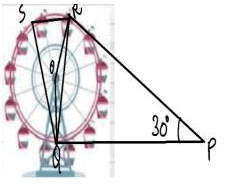
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

Q. Find ∠ORP
Detailed Solution for Test: Circles- Case Based Type Questions - Question 6
PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 7
Save

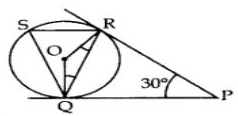
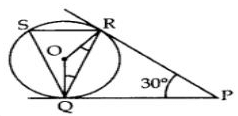
A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

Q. Find ∠RQP
Detailed Solution for Test: Circles- Case Based Type Questions - Question 7
PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 8
Save

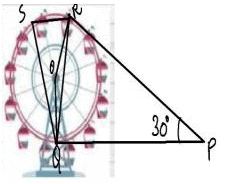
A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

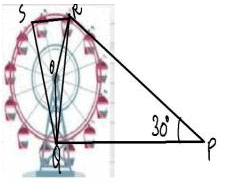
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

Q. In the given figure find ∠ROQ
Detailed Solution for Test: Circles- Case Based Type Questions - Question 8
PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 9
Save

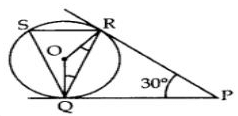
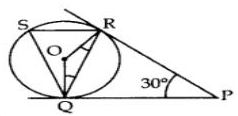
A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to the rim in such a way that as the wheel turns, they are kept upright, usually by gravity.

After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who were enjoying the ride . She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.

Q. Find ∠RSQ
Detailed Solution for Test: Circles- Case Based Type Questions - Question 9
PR = PO [∵ Tangents drawn from an external point are equal

⇒ ∠PRQ = ∠PQR [∵ Angles opposite equal sides are equal

In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180° [∆ Rule]

⇒ 30° + 2∠PQR = 180°

⇒

= 75° ⇒ SR || QP and QR is a transversal

∵ ∠SRQ = ∠PQR [Alternate interior angle]

∴ ∠SRO = 75° [Tangent is I to the radius through the point of contact]

⇒ ∠ORP = 90°

∴ ∠ORP = ∠ORQ + ∠QRP

90° = ∠ORQ + 75°

∠ORQ = 90° – 75o = 150

Similarly, ∠RQO = 15°

In ∆QOR,

∠QOR + ∠QRO + ∠OQR = 180° [∆ Rule]

∴ ∠QOR + 15° + 15° = 180°

∠QOR = 180° – 30° = 150°

⇒ ∠QSR = 12∠QO

⇒ ∠QSR = 150∘/2 = 750 [Used ∠SRQ = 75° as solved above]

In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° [∆ Rule]

∴ 75° + 75° + ∠RQS = 180°

∠RQS = 180° – 150o = 30°

Test: Circles- Case Based Type Questions - Question 10
Save

Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

Q. If radius of the circle is 4cm, Find the area of ∆OAB
Detailed Solution for Test: Circles- Case Based Type Questions - Question 10
Area ∆OAB = (1/2) * perpendicular height * Base = (1/2) * OD * AB = (1/2) * 4 * 12 = 24 cm²
Test: Circles- Case Based Type Questions - Question 11
Save

Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

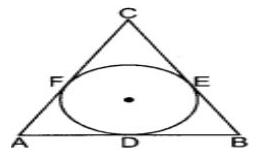
Q. Find the Length of BE
Detailed Solution for Test: Circles- Case Based Type Questions - Question 11
(x + y + z) - (x + z) = y => 15 - 10 = 5 cm = BE
Test: Circles- Case Based Type Questions - Question 12
Save

Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

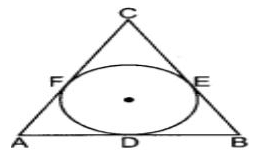
Q. Find area of ∆ABC
Detailed Solution for Test: Circles- Case Based Type Questions - Question 12
Area ∆ABC = Area ∆OAB + Area ∆OBC + Area ∆OCA

=> Area ∆ABC = [(1/2) * radius * AB] + [(1/2) * radius * BC] + [(1/2) * radius * CA]

=> Area ∆ABC = (1/2) * radius * (AB + BC + CA)

=> Area ∆ABC = (1/2) * 4 * 30

=> Area ∆ABC = 2 * 30

=> Area ∆ABC = 60 cm²

4 docs|108 tests
Join Course
Information about Test: Circles- Case Based Type Questions Page
In this test you can find the Exam questions for Test: Circles- Case Based Type Questions solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Circles- Case Based Type Questions, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 9

Download as PDF

Top Courses for Class 9

Important Questions for Circles- Case Based Type Questions

Find all the important questions for Circles- Case Based Type Questions at EduRev.Get fully prepared for Circles- Case Based Type Questions with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Circles- Case Based Type Questions syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Circles- Case Based Type Questions resources.

Circles- Case Based Type Questions MCQs with Answers

Prepare for the Circles- Case Based Type Questions within the Class 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Circles- Case Based Type Questions Class 9: Additional Practice

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Circles- Case Based Type Questions with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup