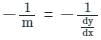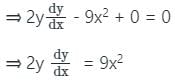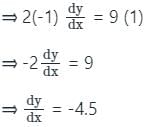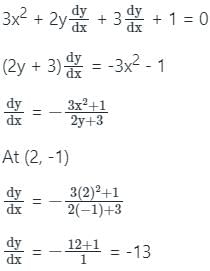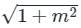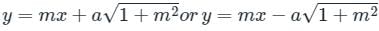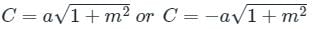Test: Circles: Tangents and Normals (9 July) - MAT MCQ
10 Questions MCQ Test - Test: Circles: Tangents and Normals (9 July)
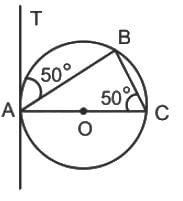
AB is a chord of a circle and AOC is its diameter such that ∠ACB = 50°, if AT is tangent to the circel at the point A, then ∠BAT is equal to
Tangent to the circle at points A and B from any external point P is represented by pair of straight lines x2 - 3y2 - 2x + 1 = 0. If O is the center of the circle then ∠ AOB will be
Find the length of the tangent from an external point such that the external point is at a distance of 13 cm from the centre of the circle of radius 5 cm ?
If the equation of one tangent to the circle with centre at (2, -1) from the origin is 3x + y = 0, then the equation of the other tangent through the origin is
If the slope and x-intercept of the line 3x − y + K = 0 are equal then what is the value of K?
Find the slope of the tangent of the curve y2 - 3x3 + 2 = 0 at (1, -1)
The number of tangents that can be drawn from (2, 6) to x2 + y2 = 40 is
The equation of the tangent to the curve x3 + y2 + 3y + x = 0 and passing through the point (2, -1).
If two circles are touching each other externally and with radii 4 and 6 cm respectively. Find the length of common tangent.
If the line y = mx + c is a tangent to the circle x2 + y2 = a2 then find condition of tangency ?


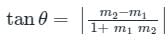

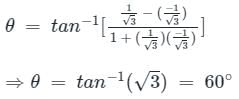

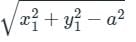
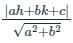
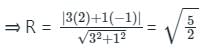
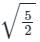 is
is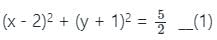
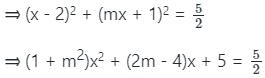
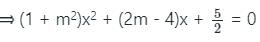 which has only one solution.
which has only one solution.