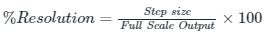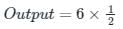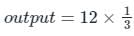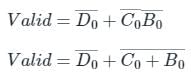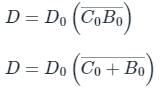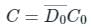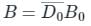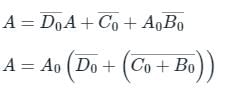Test: Code Converters - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Digital Circuits - Test: Code Converters
A 4-bit D/A converter gives an output voltage of 4.5 V for an input code of 1001. The output voltage for an input code of 0110 is
A 4 bit Digital to Analog converter (DAC) gives an output voltage of 5 V for an input code of 1111. What is the output voltage for an input code of 1100?
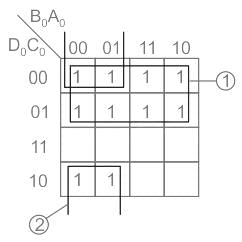
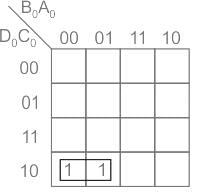
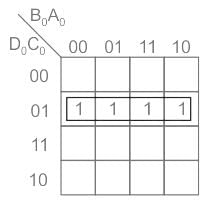
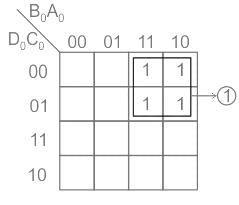
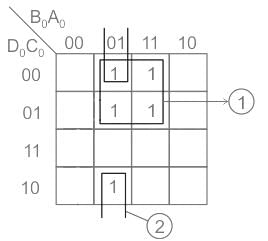
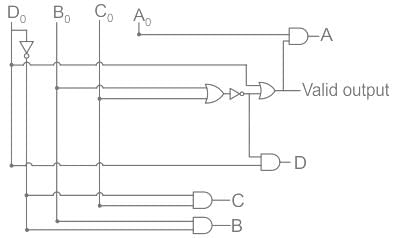
A binary-to-BCD encoder has four inputs D0 C0, B0, and A0 and five outputs D, C, B, A, and VALID. The outputs D, C, B and A give the proper BCD value of the input and the VALID output is 1 if the input combination is a valid decimal code. If the input combination is an invalid decimal code, the VALID output becomes 0, and all of the D, C, B, and A outputs show 0 values. If only NOT gates and 2-input OR and AND gates are available, the minimum number of gates required to implement the above circuit is
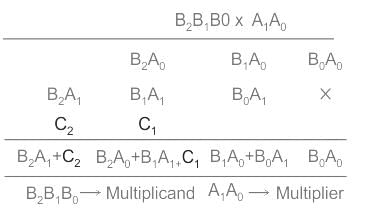
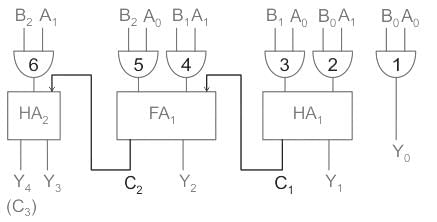
Minimum number of Half adders, Full adders, AND gates required to implement 2 × 3 multiplier is given as
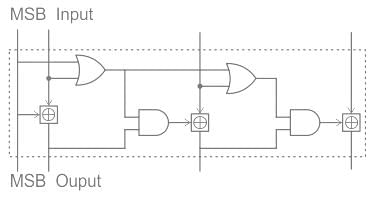
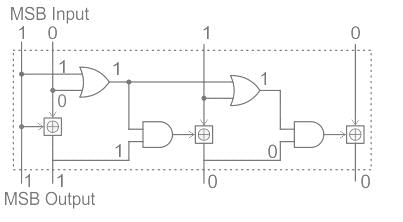
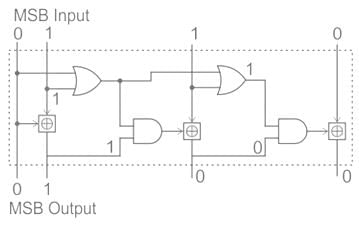
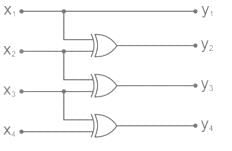
Identify the circuit below.
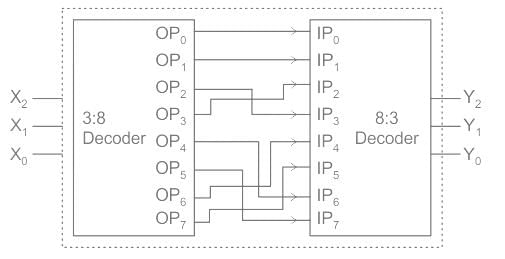
Note: Change in the above connection
OP4 is connected to IP7
OP5 is connected to IP6
Rest connections are same
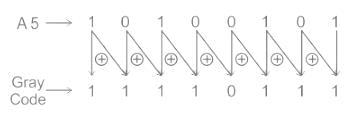
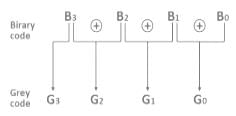
The binary representation of BCD number 00101001 (decimal 29) is
|
75 videos|145 docs|70 tests
|