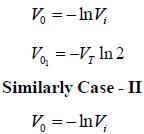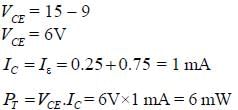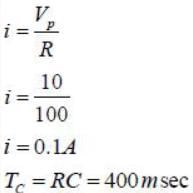Test: Combined (Thermo + Electronics) - Physics MCQ
30 Questions MCQ Test GATE Physics Mock Test Series 2026 - Test: Combined (Thermo + Electronics)
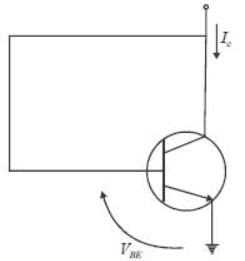
For n-p-n transistor connected as shown in figure VBE = 0.7 volts. Given that reverse saturation current of the .junction at room temperature 3000 K is 10-13 A, the emitter current is

In the bistable circuit shown in the figure, the ideal OP- Amp lias saturation levels of ±5 V. The value of R1 (in kΩ) that gives a hysteresis width of 500 mV is______

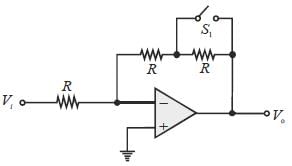
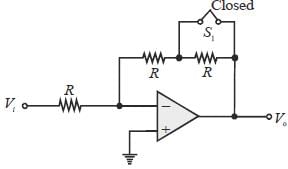
Let the magnitude of the gain in the inverting Op-Amp circuit shown be x with switch S1 open. When the switch is closed, the magnitude of gain becomes.
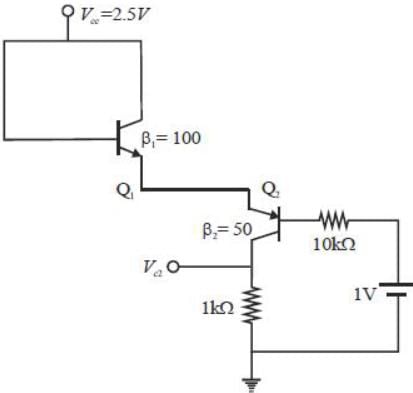
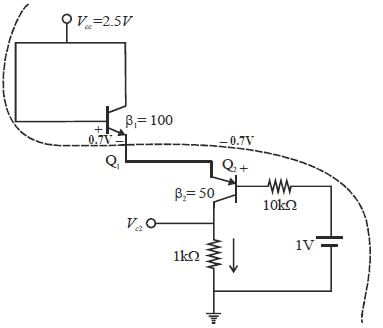
Consider the circuit shown in the figure. Assuming  the value of the dc voltage VC2 (in volt) is _____.
the value of the dc voltage VC2 (in volt) is _____.
A Weiii bridge oscillator is shown in figure, which of the following statements are true, if f " is the ffeequency of oscillation?

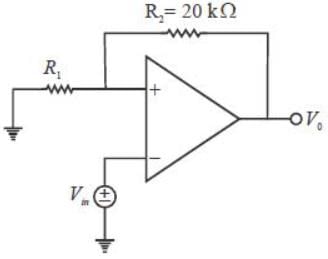
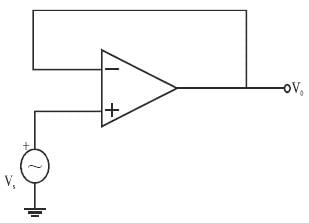
In a voltage follower op-amp circuit, find the closed loop gain V0/Vs if the open loop gain = 2
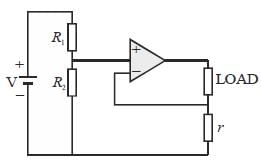
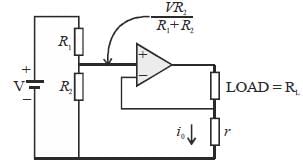
The circuit shown in figure is best described as a
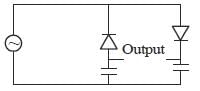
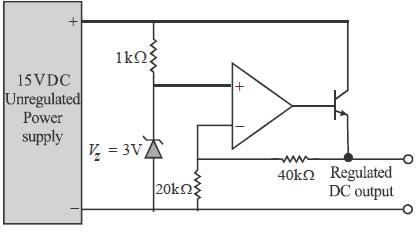
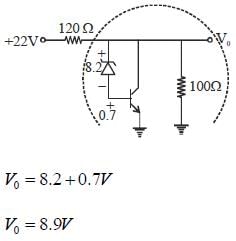
In the shunt regulator shown below, the Vz = 8.2 V and VBE = 0.7 V. The regulated output voltage V0 is
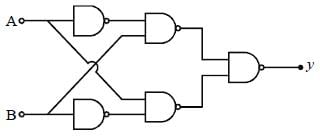
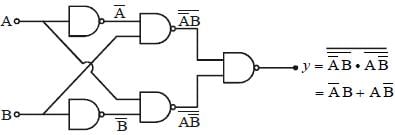
Let 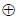 denote the Exclusive OR (XOR) operation, Let '1' and '0' denote the binary constants. Consider the following Boolean expression for F over two variables P and Q:
denote the Exclusive OR (XOR) operation, Let '1' and '0' denote the binary constants. Consider the following Boolean expression for F over two variables P and Q:
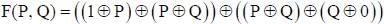
The equivalent expression for F is
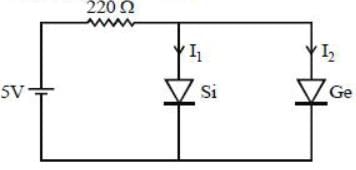
Suppose one Si and one Ge-diodes are connected in parallel and then this combination is connected to a power supply of 5 V together with a series resistance 220 Ω. The value of the current through the Si(I1) and Ge(I2) are
[Given the cut in voltage of Si diode is 0.7 V and Ge diode is 0.3 V]
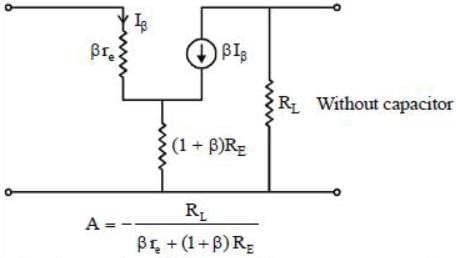
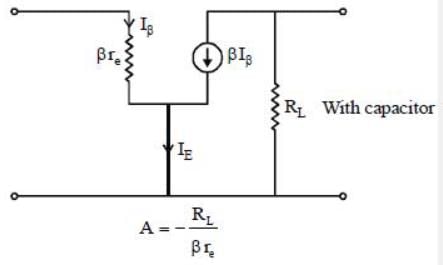
In a certain CE amplifier with emitter resistance and emitter by-pass capacitor, if the by-pass capacitor is removed the voltage gain of the amplifier.
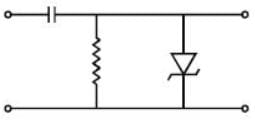
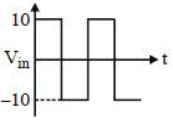
In the given circuit the time constant is larger than the period of the signal and the zener breakdown voltage of zener diode is 6V. A square wave is applied to the input as shown in figure. Which of the following graph represent the nature of the output.
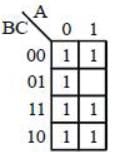
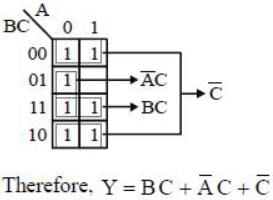
For the Karnaugh map shown in the given figure, the minimum Boolean function is:
If volume and number of particles (F, N) of a thermodynamic system are doubled, which of the following quantities is bound to be doubled?
An ideal bose gas in 5-dimensions has the energy dispersion relation ∈ = Aps. For the Bose gas to undergo Bose-Einstein condensation, which of the following should hold?
10 bosons are to be distributed in 3 different energy levels with the 2nd energy level being doubly degenerate and the other two are non-degenerate. The number of ways of achieving this is _____
For a gas confined in a box of volume V having total energy E and N number of particles, the number of microstates is 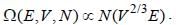 Then the equation of state is
Then the equation of state is
A real gas expands into vacuum in thermally insulated container. Winch of the following properties of the gas will not change?
Consider a system of 5 non-interacting distinguishable particles. Each particle can occupy only two energy levels ∈ and 2∈. If the total energy of the system 8∈. Then, the entropy of the system is _____ kB. (answer must be given upto 2 decimal places)
Bulk modulus of a substance is defined as 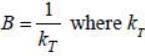 where kT is tlie isothermal compressibility. If instead kT of 1 mole of an ideal gas, we take 5 moles of the same gas, then the ratio of bulk modulus to pressure B:P =_____. (Correct answer must be given upto two place decimal)
where kT is tlie isothermal compressibility. If instead kT of 1 mole of an ideal gas, we take 5 moles of the same gas, then the ratio of bulk modulus to pressure B:P =_____. (Correct answer must be given upto two place decimal)
Water has the anomalous property that it contracts on melting. It means that
Below a certain temperature θ, the molecular specific heat of a certain gas is 5/2 kB. As the temperature is raised above θ , the specific heat becomes 7/2 kB. Which of the following can be the gas in this experiment?
For a 2nd order phase transition, which of the following remains continuous?
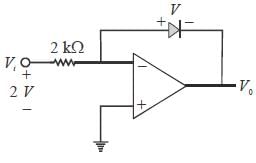
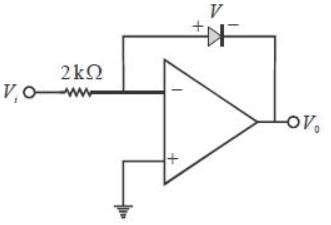
In the Op-Amp circuit shown, assume that the diode current follows the equation 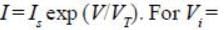
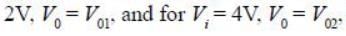 The relationship between
The relationship between 
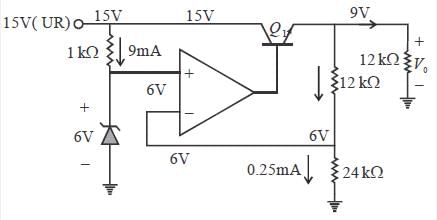
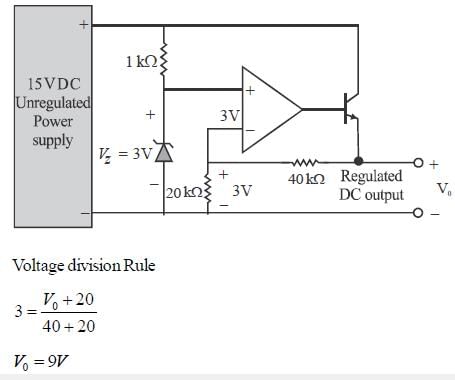
A regulated power supply, shown in figure below, lias an unregulated input (UR) of 15 volts and generates a regulated ouput. Use the component values shown in the figure.
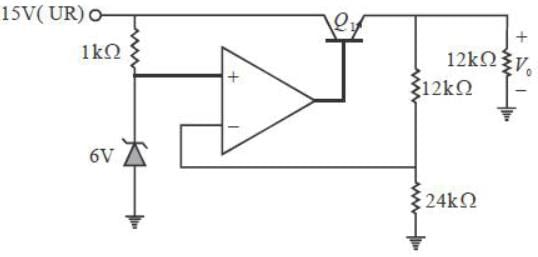
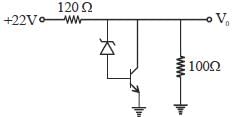
The power dissipation across the transistor Q1 shown in the figure is
The output voltage of the regulated power supply shown in figure is
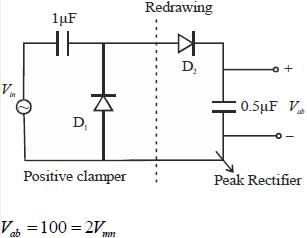
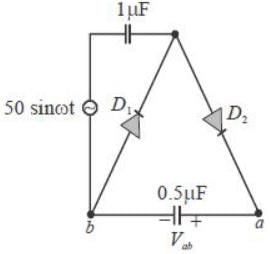
Ill the circuit shown, assume that diodes D1 and D2 are ideal. In the steady-state condition, the average voltage Vab ( in Volts) across the 0.5 μF capacitor is ______
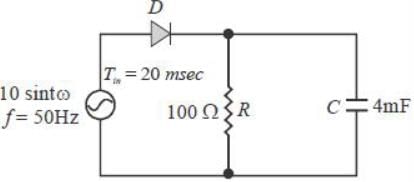
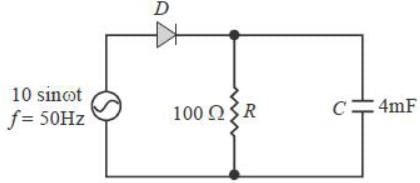
The figure shows a half-wave rectifier. The diode D is ideal. The average steady state current (in Amperes) through the diode is approximately______
|
1 docs|34 tests
|


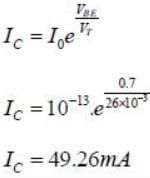
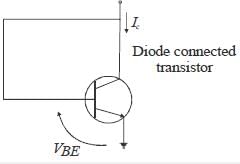
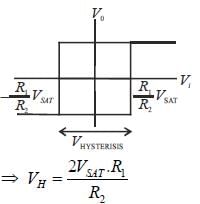
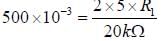
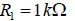

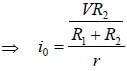

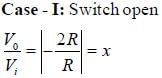
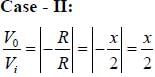
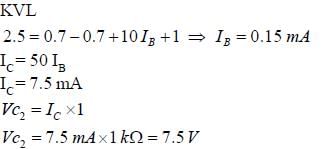


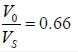

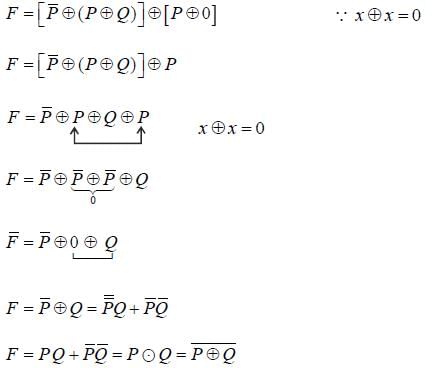
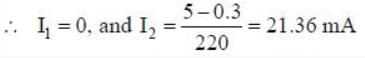
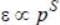 (S > 0 because increasing momentum should not decrease energy), we have
(S > 0 because increasing momentum should not decrease energy), we have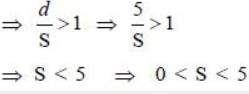
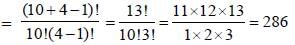
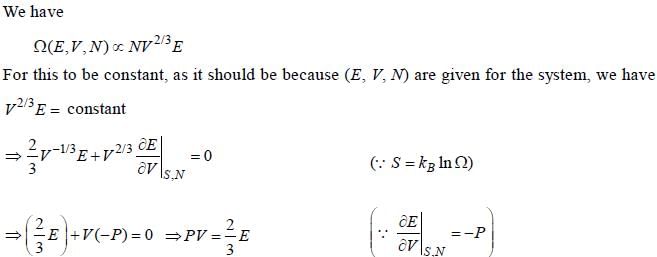

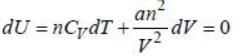
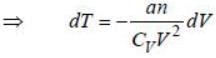

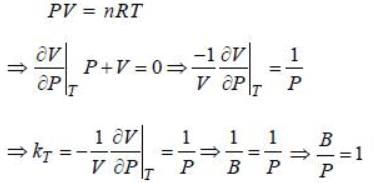
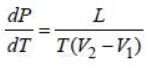
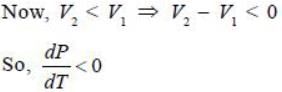
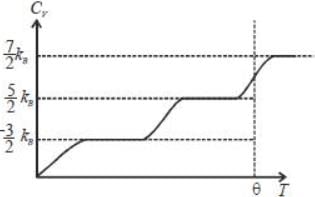
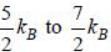 comes from vibrational degrees of freedom.
comes from vibrational degrees of freedom.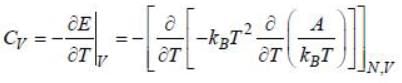
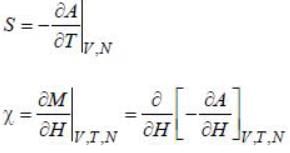
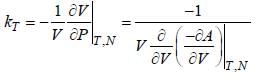
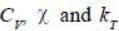 are 2nd order derivatives of free energy A, they are discontinuous. Moreover, entropy is continuous across 2nd order phase transition.
are 2nd order derivatives of free energy A, they are discontinuous. Moreover, entropy is continuous across 2nd order phase transition.