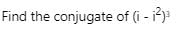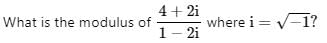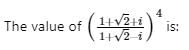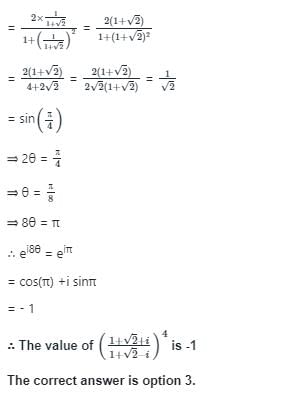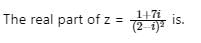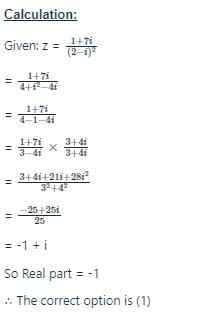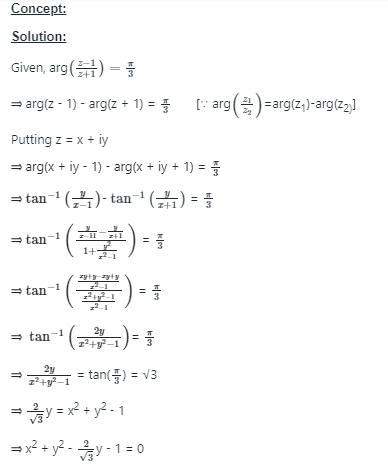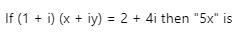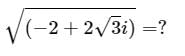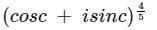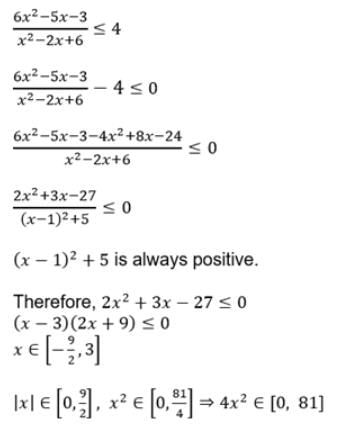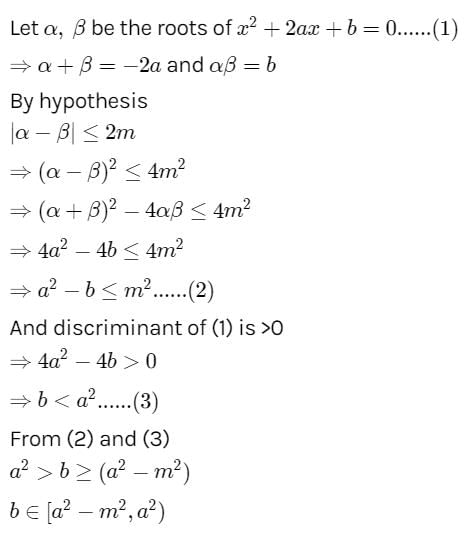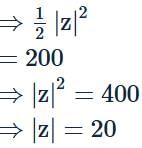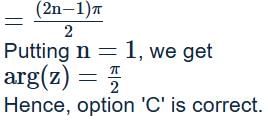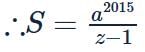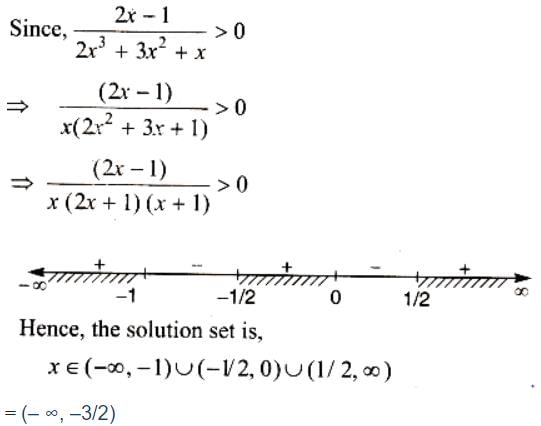Test: Complex Numbers
30 Questions MCQ Test Mathematics (Maths) Class 11 | Test: Complex Numbers
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Number of values `p' for which the equation (p2 – 3p + 2) x2 – (p2 – 5p + 4)x + p – p2 = 0 possess more than two roots, is
The roots of the equation (b – c) x2 + (c – a) x + (a – b) = 0 are
Clearly, x = 1 is a root of the given equation.
Let, alpha, beta are the roots ; alpha = 1
We know , product of the roots :-
Alpha * Beta = a-b / b-c
1* ( beta) = a-b / b- c
Beta = a-b/ b- c
Therefore, roots are :- ( a-b/b-c, 1)
If a, b are the roots of quadratic equation x2 + px + q = 0 and g, d are the roots of x2 + px – r = 0, then (a – g) . (a - d) is equal to
x2+px+q=0 have roots a,b
a=b=-p --(1)
ab = q --(2)
a2+pa+q=0 --(3)
x2+px−r=0 have roots g,d
g+d=-p --(4)
gd = -r --(5)
(a-g)(a-d) = a2−(g−d)a+gd
= a2+pa−r = -q-r =-(q+r) --from (3)
Therefore -(q+r) id the answer.
Two real numbers a & b are such that a + b = 3 & |a - b| = 4, then a & b are the roots of the quadratic equation
If a, b, c are integers and b2 = 4(ac + 5d2), d ∈ N, then roots of the equation ax2 + bx + c = 0 are
b2 = 4(ac + 5d2)
D = b2 − 4ac
= 4(ac + 5d2) − 4ac
= 4ac + 20d2 − 4ac
= 20d2
Now, x = (−b ± √D)/2a
=(− b ± √20d2)/2a
=(− b ± 2√5d)/2a
Therefore, roots of the given quadratic equation are irrational.
Let a, b and c are real numbers such that 4a + 2b + c = 0 and ab > 0. Then the equation ax2 + bx + c = 0 has
Put x=2 in the LHS of the quadratic equation
We get, 4a + 2b + c = 0
Hence x=2 is a root of the equation. (Real roots)
Which of the following graph represents expression f(x) = ax2 + bx + c (a < 0) when a > 0, b < 0 & c < 0 ?
The expression y = ax2 + bx + c has always the same sign as of `a' if
For the quadratic curve to always have the same sign, it must never cut the X-axis, i i.e. it must not have any real roots.
So, b2 – 4ac < 0
4ac > b2
If a, b ∈ R, a < 0 and the quadratic equation ax2 – bx + 1 = 0 has imaginary roots then a + b + 1 is
f(x) = ax2 - bx + c
f(0) = 1 (positive)
That is, f(x) = ax2 - bx + 1 = 0
Therefore f(x) has imaginary roots
f(-1) = a+b+c > 1 (Hence positive)
If a and b are the non–zero distinct roots of x2 + ax + b = 0, then the least value of x2 + ax + b is
ANSWER :- c
Solution :- a and b of x^2 + ax + b = 0
Sum of roots : a + b = -a, 2a + b = 0
Product of roots : ab = b, b(a-1)
Minimum value of x^2 + ax + b at x =-a/2
We get a = -9/4
y = -2x2 - 6x + 9
dy/dx = -4x - 6
Put dy/dx = 0
-4x - 6 = 0
x = -3/2 = 1.5
d2y/dx2 = -4 < 0 (Maximum point)
Max value = -2(-1.5)2 - 6(-1.5) + 9
= 13.5
Max value of x = -1.5
The number of the integer solutions of x2 + 9 < (x + 3)2 < 8x + 25 is
If both roots of the quadratic equation (2 – x) (x + 1) = p are distinct & positive, then p must lie in the interval
The RHS of the expression has a<0 which means the graph will lie below the x-axis and πx lies above the x-axis.Therefore,no solution.
Let a > 0, b > 0 and c > 0. Then both the roots of the equation ax2 + bx + c = 0
The set of all solutions of the inequality 
< 1/4 contains the set
(1/2)(x2 - 2x) < (1/4)
(1/2)(x2 - 2x) < (1/2)2
x2 − 2x > 2......(as after multiplicative inverse sign of inequality changes)
x2 − 2x − 2 > 0
x2 - 2x + 1 - 3 >
(x-1)2 - 3 > 0
(x-1)2 > 3
So for the above to hold good both the expression must be positive or both must be negative. After finding the solution the range of the solution will be
either x > 3
(3,¥)
Consider y =
, where x is real, then the range of expression y2 + y – 2 is
The values of k, for which the equation x2 + 2(k – 1) x + k + 5 = 0 possess atleast one positive root, are
<= 4, then least and the highest values of 4x2 are
If coefficients of the equation ax2 + bx + c = 0, a < 0 are real and roots of the equation are non–real complex and a + c + b < 0, then
Puting x=-1
a-b+c
but
a+c<b or a+c-b<0
hence f(x)<0 for all real values of x
therefore
putting x=-2
we get f(X)=4a+c-2b<0
or 4a+c<2b
If the roots of the equation x2 + 2ax + b = 0 are real and distinct and they differ by at most 2m, then b lies in the interval
If the roots of the quadratic equation x2 + px + q = 0 are tan 30º and tan 15º respectively, then the value of 2 + q – p is
If (1 – p) is root of quadratic equation x2 + px + (1 – p) = 0, then its roots are
As (1 – p) is root of the equation: x2 + px + (1 – p) = 0
(1 – p)2 + p(1 – p) + (1 – p) = 0
(1 – p)[1 – p + p + 1] = 0
(1 – p) = 0
p = 1
Therefore, given equation now becomes
x2 + x = 0
x(x + 1) = 0
x = 0, -1
The values of x and y besides y can satisfy the equation (x, y ∈ real numbers) x2– xy + y2 – 4x – 4y + 16 = 0
For what value of a and b the equation x4 – 4x3 + ax2 + bx + 1 = 0 has four real positive roots ?
Since all roots are positive,
coeff. of x shld be negatuve i.e., b is negative
let roots be m(>0), n(>0), p(>0), q(>0)
m+n+p+q = 4
mn+np+pq+mp+mq+nq = a
mnp+mnq+npq+mpq = -b
mnpq = 1
For the objective case,
put m=n=p=q =1
so a = 1+1+1+1+1+1 = 6
-b = 1+1+1+1 =4
so, a = 6 and b = -4
If a, b are roots of the equation ax2 + bx + c = 0, then the value of a3 + b3 is
The numbers in the questions are not very clear.
z1 = 2 + i
z2 = 1+3i
z1 – z2 = (2 – 1) + i (1 – 3)
= 1 – 2i
If a, b are roots of the equation ax2 + bx + c = 0 then the equation whose roots are 2a + 3b and 3a + 2b is
If S is the set of all real x such that 
is positive, then S contains
If the roots of the equation x2 - 5x + 16 = 0 are a, b and the roots of the equation x2 + px + q = 0 are (a2 + b2) and 
, then-
|
156 videos|176 docs|132 tests
|
|
156 videos|176 docs|132 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
