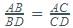Test: Construction of Tangents - CAT MCQ

If TP and TQ are two tangents to a circle with centre O so that angle POQ = 110° then angle PTQ is equal to

​

D and E are the mid points of sides AB and AC respectively of a triangle ABC such that DE is parallel to BC. If AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x-1) cm, then the value of x is 

PQ is a tangent to a circle with centre O at the point P. If triangle OPQ is an isosceles triangle, then angle OQP is equal to​ 

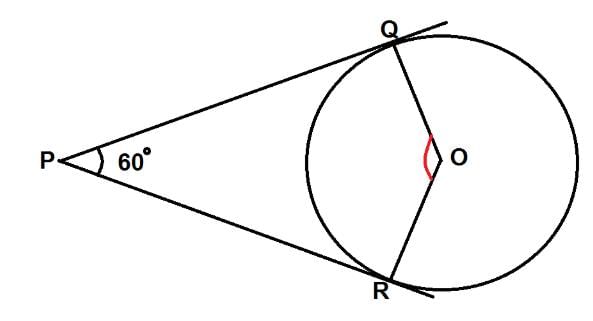
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at the end points to those two radii of the side, the angle between which is​

To draw a pair of tangents to a circle which are inclined to each other at an angle of 45° it is required to draw tangents at the end point of those two radii of the circle, the angle between which is :​

A point O is at a distance of 10 cm from the centre of a circle of radius 6 cm. How many tangents can be drawn from point O to the circle?

Length of the tangent to a circle from a point 26 cm away from the centre is 24 cm. What is the radius of the circle?​