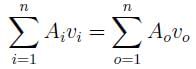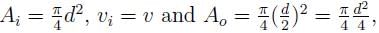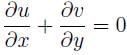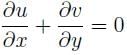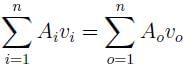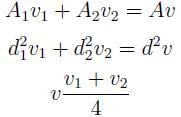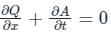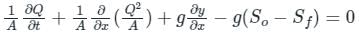Test: Continuity Equation
10 Questions MCQ Test Fluid Mechanics for Civil Engineering | Test: Continuity Equation
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a liquid enters a pipe of diameter d with a velocity v, what will it’s velocity at the exit if the diameter reduces to 0.5d?
According to the Continuity Equation,
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions.
If, 
vo = 4v
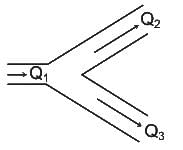
Two pipes, each of diameter d, converge to form a pipe of diameter D. What should be the relation between d and D such that the flow velocity in the third pipe becomes double of that in each of the two pipes?
According to the Continuity Equation,
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,
A1v1 + A2v2 = Av
d2v + d2v = D2v
D = d.
In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax2 + bxy + cy2 and v = cxy. What should be the condition for the flow field to be continuous?
According to the condition for continuity,
2ax + cx = 0
2a + c = 0.
In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax2 + bxy and v = bxy + ay2. The condition for the flow field to be continuous is
The condition for the flow field to be continuous is:
2ax + by + 2ay + bx = 0
x + y = 0
Hence, the condition for the flow field to be continuous is independent of the constants (a; b) and dependent only on the variables (x; y).
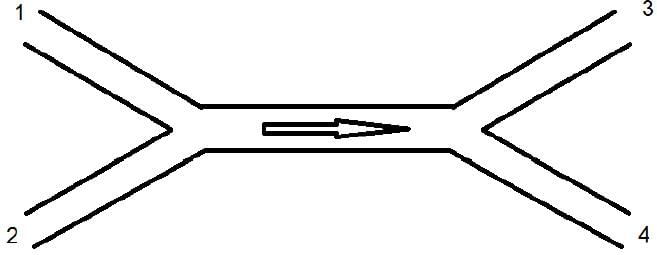
In a water supply system, water flows in from pipes 1 and 2 and goes out from pipes 3 and 4 as shown. If all the pipes have the same diameter, which of the following must be correct?
According to the Continuity Equation,
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions.
A1v1 + A2v2 = A3v3 + A4v4
Since d1 = d2 = d3 = d4, v1 + v2 = v3 + v4.
According to the Continuity Equation, if no fluid is added or removed from the pipe in any length then the mass passing across different sections shall be the same. This is in accordance with the principle of conservation of mass which states that matter can neither be created nor be destroyed.
Two pipes of diameters d1 and d2 converge to form a pipe of diameter 2d. If the liquid flows with a velocity of v1 and v2 in the two pipes, what will be the flow velocity in the third pipe?
According to the Continuity Equation,
where a represents flow area, v represents flow velocity, i is for inlet conditions and o is for outlet conditions. Thus,
St. Venant Equations:
1. Continuity equation
2. Momentum Equation
Assumptions for St. Venant Equations
- Flow is one-dimensional
- Hydrostatic pressure prevails and vertical accelerations are negligible
- Streamline curvature is small.
- Bottom slope of the channel is small.
- Manning’s equation is used to describe resistance effects
- The fluid is incompressible
Hence, St. venant equations represent continuity and momentum equations.
A fluid flowing through a pipe of diameter 450 mm with velocity 3 m/s is divided into two pipes of diameters 300 mm and 200 mm. The velocity of flow in 300 mm diameter pipe is 2.5 m/s, then the velocity of flow through 200 mm diameter pipe will be
Concept:
According to continuity, the liquid flow rate will be conserved.
Q1 = Q2 + Q3
In a pipe, flow rate is given by
Q = AV
Calculation:
Given V1 = 3 m/s, D1 = 450 mm, V2 = 2.5 m/s, D2 = 300 mm, D3 = 200 mm;
From continuity,
D12 V1 = D22 V2 + D32 V3
⇒ 4502 × 3 = 3002 × 2.5 + 2002 × V3
⇒ V3 = 9.56 m/s
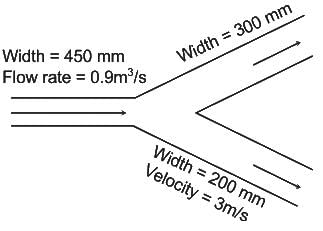
A channel of width 450 mm branches into two sub-channels having width 300 mm and 200 mm as shown in figure. If the volumetric flow rate (taking unit depth) of an incompressible flow through the main channel is 0.9 m3/s and the velocity in the sub-channel of width 200 mm is 3 m/s, the velocity in the sub-channel of width 300 mm is ______m/s
Assume both inlet and otlet to be at the same elevation.
Concept:
The principle used here is Conservation of mass
∴ Q1 = Q2 + Q3
Calculation:
Q1 = Q2 + Q3
A1V1 = A2V2 + A3V3
⇒ 0.9 = 300 × 10-3 × V2 + 200 × 10-3 × 3
⇒ 0.9 = 0.3 V2 + 0.6
⇒ V2 = 1 m/s
|
43 videos|73 docs|87 tests
|
|
43 videos|73 docs|87 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
