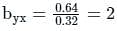Test: Correlation - 2 - Commerce MCQ
15 Questions MCQ Test - Test: Correlation - 2
The coefficient of correlation between ages of husband and wife at the time of marriage for a given set of 100 couples was noted to be 0.7. Assume that all these couples survive to celebrate the silver jubilee of their marriage. The coefficient of correlation at that point of time will be
Directions: Read the following information and answer the two items that follow:
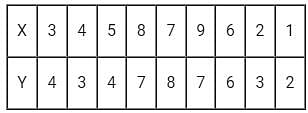
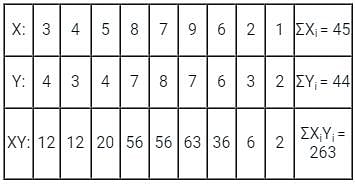
Consider the table

The two regression coefficients byx and bxy respectively are
Consider the table

The two regression coefficients byx and bxy respectively are
Comprehension:
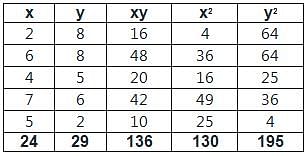
For the following data

Regression equation of X on Y
For the following data

Regression equation of X on Y
Given x = 2y + 4 and y = kx + 6 are the lines of regression of x on y and y on x respective.
Find the value of k, if value of r is 0.5.
For two correlated variables x and y, if coefficient of correlation between x and y is 0.8014, variance of x and y are 16 and 25 respectively. Then the covariance between x and y is:
If the correlation coefficient between X and Y is 0.8 and covariance is 121 and the variance of Y is 64, then variance of X will be
If byx = 0.5, bxy = 0.46, then the value of Correlation coefficient (r) is –
Given two lines of regression x + 3y = 11 and 2x + y = 7. Find the coefficient of correlation between x and y.
Following two statements are related to regression coefficient
(I) Independent of the change of origin
(II) Independent of the change of scale
For two variables x and y, the two regression coefficients are byx = -3/2 and bxy = -1/6. The correlation coefficient between x and y is:
If x̅ = 25, y̅ = 120, bxy = 2. Find the value of x when y = 130
Comprehension:
For the following data

If the regression equation of Y on X is Y= 0.929X + 7.284, then correlation coefficient is
If r = 0.8, bxy = 0.32, then what will be the value of byx.


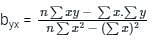
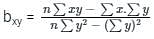

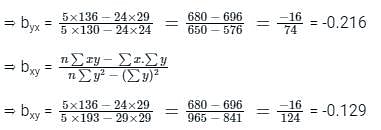

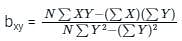

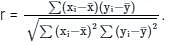


 (On squaring both sides)
(On squaring both sides)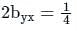
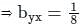
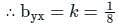
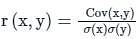
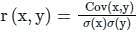
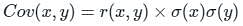
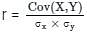
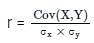
 since Var X = 64, then σy = √64 = 8
since Var X = 64, then σy = √64 = 8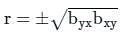
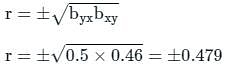
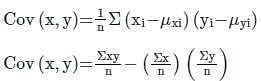
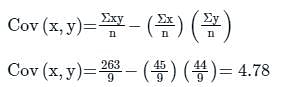

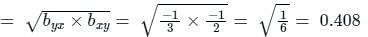
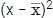 is calculated, it remains unaffected. But, change of scale alters all values unevenly and hence, variation changes.
is calculated, it remains unaffected. But, change of scale alters all values unevenly and hence, variation changes. 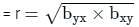
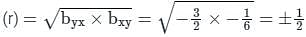
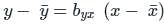 where byx is called the regression coefficient of y on x.
where byx is called the regression coefficient of y on x.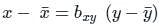 where bxy is called the regression coefficient of x on y.
where bxy is called the regression coefficient of x on y.
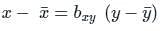
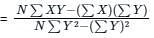
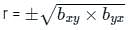


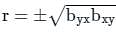
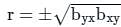
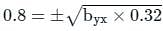 (On squaring both the sides)
(On squaring both the sides)