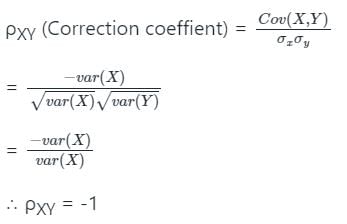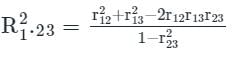Test: Correlation Analysis - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Correlation Analysis
The multiple correlation coefficient R1,23 as compared to any simple correlation coefficients between the distinct variable X1 ,X2, and X3 is
For a trivariate distribution, if the correlation coefficients are r12 = r13 = r23 = r, -1 < r < 1, then r12.3 is:
If a data set contains n paired values on two variables x(independent) and y(dependent), then their plot is called:
If the regression line of Y on X is Y = 30 - 0.9X and the standard deviations are Sx = 2 and Sy = 9, then the value of the correlation coefficient rxy is:
The correlation coefficient between two variables X and Y is 0.4. The correlation coefficient between 2X and (-Y) will be:
For an experiment we have the following data set: n = 4, ∑x = a, ∑y = 10, ∑xy = 21, ∑x2 = 30, ∑y2 = 30. If the correlation coefficient is -0.8 then the value of a is:
An experiment consists of tossing a coin 20 times. Such an experiment is performed 50 times. The number of heads and the number of tails in each experiment are noted. What is the correlation coefficient between the two?
Match List - I with List - II
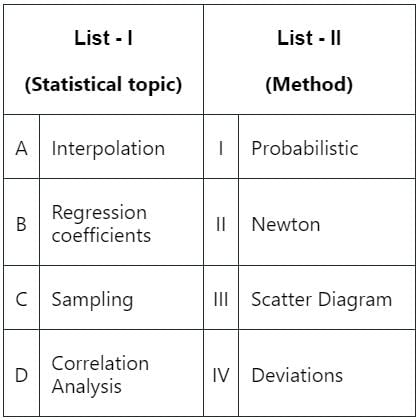
Choose the correct answer from the options given below:
The coefficient of correlation between two variables X and Y is 0.48. The covariance is 36. The variance of X is 16. The standard deviation of Y is:
If the multiple correlation coefficient of X1 on X2 and X3 is zero, then: