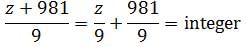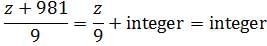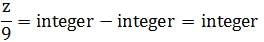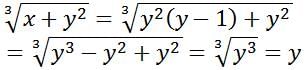Test: Data Sufficiency - 4 - GMAT MCQ
10 Questions MCQ Test - Test: Data Sufficiency - 4
If w, x, y, and z are the digits of the four-digit number N, a positive integer, what is the remainder when N is divided by 9?
1) w + x + y + z = 13
2) N + 5 is divisible by 9
1) w + x + y + z = 13
2) N + 5 is divisible by 9
After a long career, John C. Walden is retiring. If there are 25 associates who contribute equally to a parting gift for John in an amount that is an integer, what is the total value of the parting gift?
1) If four associates were fired for underperformance, the total value of the parting gift would have decreased by $200
2) The value of the parting gift is greater than $1,225 and less than $1,275
1) If four associates were fired for underperformance, the total value of the parting gift would have decreased by $200
2) The value of the parting gift is greater than $1,225 and less than $1,275
If x and y are positive integers, what is the value of x?
(1) Twice x equals 4 times y.
(2) xy is the square of a positive integer
(1) Twice x equals 4 times y.
(2) xy is the square of a positive integer
If z = xn-19, is z divisible by 9?
1)x = 10; n is a positive integer
2)z + 981 is a multiple of 9
x is a positive integer; what is the value of x?
1)The sum of any two positive factors of x is even
2)x is a prime number and x < 4
What is the value of x?
1)The average (arithmetic mean) of 5, x2, 2, 10x, and 3 is -3
2)The medianof 109, -32, -30, 208, -15, x, 10, -43, 7 is -5
In 2003, a then-nascent Internet search engine developed an indexing algorithm called G-Cache that retrieved and stored X million webpages per hour. At the same time, a competitor developed an indexing algorithm called HTML-Compress that indexed and stored Y million pages per hour. If both algorithms indexed a positive number of pages per hour, was the number of pages indexed per hour by G-Cache greater than three times the number of pages indexed by HTML-Compress?
1)On a per-hour basis in 2003, G-Cache indexed 1 million more pages than HTML-Compress indexed
2)HTML-Compress can index between 400,000 and 1.4 million pages per hour

If angle ABC is 30 degrees, what is the area of triangle BCE?
1)Angle CDF is 120 degrees, lines L and M are parallel, and AC = 6, BC = 12, and EC = 2AC
2)Angle DCG is 60 degrees, angle CDG is 30 degrees, angle FDG = 90, and GC = 6, CD = 12 and EC = 12
If both x and y are positive integers less than 100 and greater than 10, is the sum x + y a multiple of 11?
1)x -y is a multiple of 22
2)The tens digit and the units digit of x are the same; the tens digit and the units digit of y are the same
If x and y are positive integers, is the following cube root an integer?
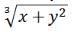
1)x = y2(y-1)
2)x = 2