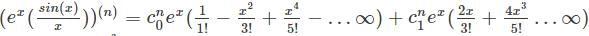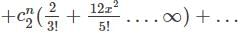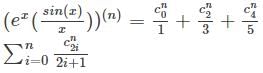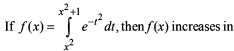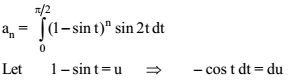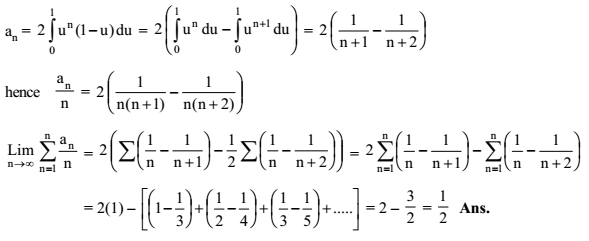Test: Definite Integration: Leibnitz Theorem (3 Oct) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Test: Definite Integration: Leibnitz Theorem (3 Oct)
Let f(x) = sin(x)/1+x2. Let y(n) denote the nth derivative of f(x) at x = 0 then the value of y(100) + 9900y(98) is
Let f(x) = ln(x)/x+1 and let y(n) denote the nth derivative of f(x) at x = 1 then the value of 2y(100) + 100y(99)
Let f(x) = 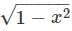 and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) is
and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) is
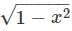 and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) is
and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) isLet f(x) = tan(x) and let y(n) denote the nth derivative of f(x) then the value of y(9998879879789776) is
If the first and second derivatives at x = 0 of the function f(x)= 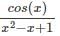 were 2 and 3 then the value of the third derivative is
were 2 and 3 then the value of the third derivative is
For the given function f(x)= 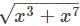 the values of first and second derivative at x = 1 are assumed as 0 and 1 respectively. Then the value of the third derivative could be
the values of first and second derivative at x = 1 are assumed as 0 and 1 respectively. Then the value of the third derivative could be
Let f(x)= 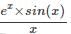 and let the nth derivative at x = 0 be given by y(n) Then the value of the expression for y(n) is given by
and let the nth derivative at x = 0 be given by y(n) Then the value of the expression for y(n) is given by
Let f(x) = ex sinh(x) / x, let y(n) denote the nth derivative of f(x) at x = 0 then the expression for y(n) is given by
|
360 tests
|


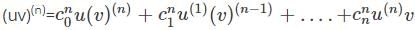
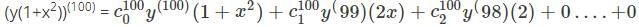
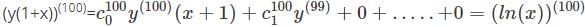
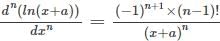
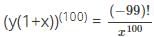
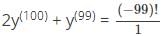

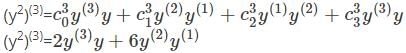
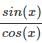
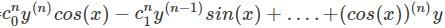
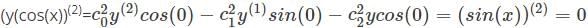
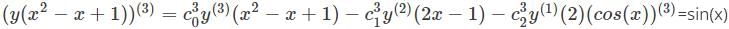
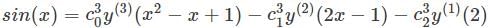
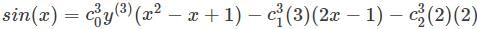
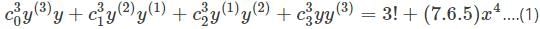
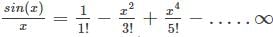
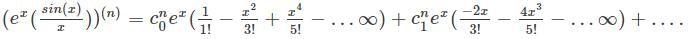
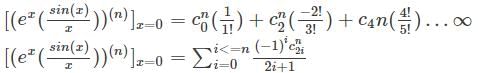
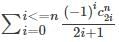 is the right answer.
is the right answer.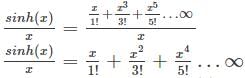
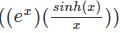 applying the Leibniz rule for nth derivative we have
applying the Leibniz rule for nth derivative we have