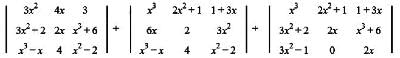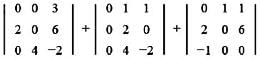Test: Determinants - 1 - JEE MCQ
25 Questions MCQ Test - Test: Determinants - 1
If A is a non singular matrix of order 3 , then |adj(A3)| =
Let A = 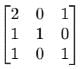 B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and
B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and 
If α = |B| and β is the sum of all the diagonal elements of B, then α2 + β2 is equal to
Let for any three distinct consecutive terms a, b, c of an A.P, the lines ax + by + c = 0 be concurrent at the point P and Q(α, β) be a point such that the system of equations
x + y + z = 6,
2x + 5y + αz = β and
x + 2y + 3z = 4,
has infinitely many solutions. Then (PQ)² is equal to ____.
Consider the system of linear equations
x + y + z = 4μ,
x + 2y + 2λz = 10μ,
x + 3y + 4λ²z = μ² + 15
where λ, μ ∈ R.
Which one of the following statements is NOT correct?
Consider the system of linear equations
x + y + z = 5,
x + 2y + λ²z = 9,
x + 3y + λz = μ, where λ, μ ∈ R.
Then, which of the following statement is NOT correct?
If the system of linear equations
x - 2y + z = -4
2x + αy + 3z = 5
3x - y + βz = 3
has infinitely many solutions, then 12α + 13β is equal to
If the system of equations
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to
If the entries in a 3 x 3 determinant are either 0 or 1 , then the greatest value of this determinant is :
The system of equations given is:x + 2y + 3z = 34x + 3y - 4z = 48x + 4y - λz = 9 + μThe question asks for the ordered pair (λ, μ) when the system has infinitely many solutions.
Let S₁ and S₂ be respectively the sets of all a ∈ ℝ - {0} for which the system of linear equations
ax + 2ay - 3az = 1
(2a + 1)x + (2a + 3)y + (a + 1)z = 2
(3a + 5)x + (a + 5)y + (a + 2)z = 3
has unique solution and infinitely many solutions. Then
In a third order determinant, each element of the first column consists of sum of two terms, each element of the second column consists of sum of three terms and each element of the third column consists of sum of four terms. Then it can be decomposed into n determinants, where n has value
The given system of equations is:
ax + 2y + z = 1
2ax + 3y + z = 1
3x + ay + 2z = β
For some α, β ∈ ℝ. The question asks which of the following is NOT correct.


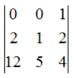
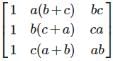 , then Det. A is
, then Det. A is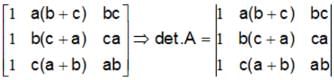
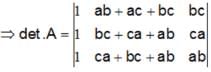
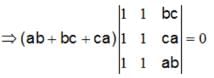
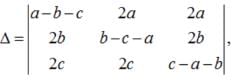
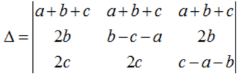
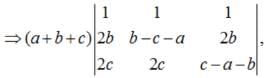
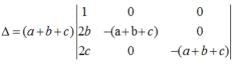

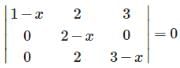 are
are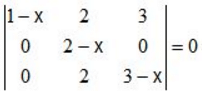
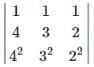 is equal to
is equal to 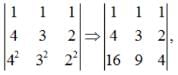
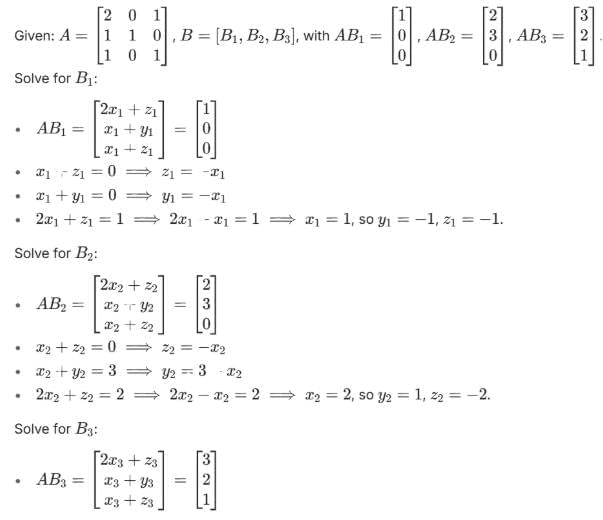

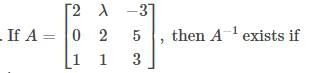
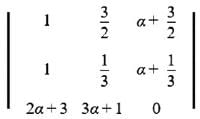 lie in the interval
lie in the interval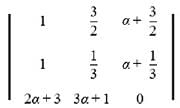 = 0
= 0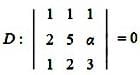
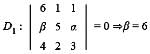
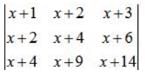

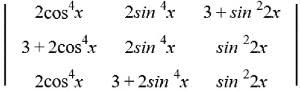 then (1/5) f'(0) is equal to
then (1/5) f'(0) is equal to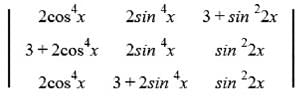
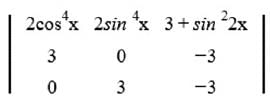
 = = (2λ - 1)²
= = (2λ - 1)²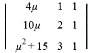
 = 0
= 0 = 0 = μ = 13
= 0 = μ = 13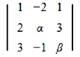
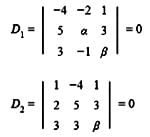
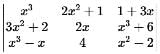 for all x ∈ R, then 2f(0) + f'(0) is equal to
for all x ∈ R, then 2f(0) + f'(0) is equal to = 0
= 0