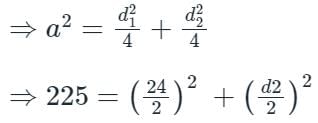Test: Diagonals - GMAT MCQ
10 Questions MCQ Test - Test: Diagonals
The length of a rectangular field is twice its breadth. If the area of the field is 288 sq.m., the length of the field is:
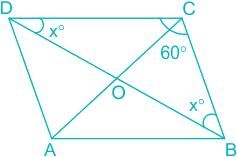
In the given figure, ABCD is a rhombus in which ∠C = 60°. Then, find the value of AC : BD.

The difference between the interior and exterior angle at a vertex of a regular polygon is 144°. What is the number of sides of the polygon?
If the external angle of a polygon is 45° then find the number of diagonal in this polygon.
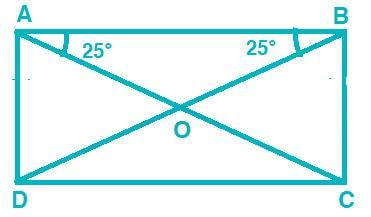
The diagonals of a rectangle are inclined to one side of the rectangle at 25°. The acute angle formed between the diagonals is:
Side of a rhombus is 15 cm and the length of its diagonal is 60% more than the length of its side. What is the length of the other diagonal of the rhombus?
Find the number of sides of a polygon whose sum of all interior angle is 2160°?
If the measure of each interior angle of a regular polygon is 150°, then the number of its diagonals will be
The length of two parallel sides of a trapezium are 53 cm and 68 cm respectively, and the distance between the parallel sides is 16 cm. Find the area of the trapezium.
If each interior angle of a regular polygon is 135°, then find the number of diagonals of the polygon.