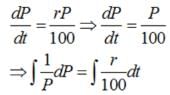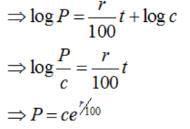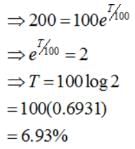Test: Differential Equations- 1 - JEE MCQ
25 Questions MCQ Test - Test: Differential Equations- 1
Differential equations are equations containing functions y = f(x), g(x) and
General solution of a differential equation of order n contains how many arbitrary constants?
Differential equation of the family of circles touching the y-axis at origin is
Which of the following is a homogeneous differential equation?
Particular solution of a given differential equation
Find a particular solution of = y tanx; y = 1 when x = 0
Differential equation of the family of parabolas having vertex at origin and axis along positive y-axis is
A first order linear differential equation. Is a differential equation of the form
Degree of a differential equation, when the equation is polynomial equation in y′ is
The number of arbitrary constants in the general solution of a differential equation of fourth order are:
For the differential equation xy = (x+2) (y+2) find the solution curve passing through the point (1, –1).
Differential equation of the family of ellipses having foci on y-axis and centre at origin is
The number of arbitrary constants in the particular solution of a differential equation of third order are:
Find the particular solution of the differential equation log = 3x+4y, given that y = 0 and x = 0.
Find the equation of a curve passing through the point (0, 0) and whose differential equation is y′ = ex sin x.
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
Find the equation of a curve passing through the point (0, –2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.